В настоящее время практически каждый человек старается окружить себя полезными и красивыми вещами, одной из которых является компьютерная графика (ее можно встретить в печатной литературе, на экране телевизора и рекламном плакате, дизайнерском проекте). С развитием компьютерных технологий компьютерная графика все больше проникает в жизни людей, она используется в науке и образовании, бизнесе, киноиндустрии, а также во всевозможных отраслях промышленности [1]. Но не стоит забывать, что изучение компьютерной графики далеко не легкий процесс [2, 3, 4]. В данной статье мы рассмотрим одну из наиболее сложных задач компьютерной графики — удаление невидимых линий и поверхностей.
В процессе отображения трехмерной сцены на экране может возникнуть такая ситуация, когда часть объектов сцены перекрывает другие объекты. Невидимые наблюдателю части объектов не должны быть отображены на экране, или должны рисоваться особым образом (например, пунктиром). Неправильная отрисовка видимых и невидимых линий может привести к искажению изображения (к его неправильному восприятию). Выход из подобных ситуаций можно найти с помощью алгоритмов удаления линий и поверхностей. Невидимые линии удаляются при отображении сцены в каркасном виде (алгоритм выделяет части ребер объекта, которые заслонены и удаляет их). При отображении объектов с помощью закрашенных поверхностей удаляются их невидимые части. Также определяются видимые и невидимые для наблюдателя части объемов, которые могут быть удалены аналогичным образом [3].
В настоящее время существует множество алгоритмов удаления невидимых линий и поверхностей. Все их можно разделить на три группы:
- алгоритмы, работающие в пространстве объекта (например, алгоритм Робертса);
- алгоритмы, работающие в пространстве изображения (алгоритм Коэна-Сазерленда, алгоритм с использованием z-буфера, алгоритм Варнока, Алгоритм Вейлера-Азертона и другие);
- алгоритмы, работающие попеременно с системами координат как объекта, так и изображения (алгоритм Ньюэла-Ньюэла-Санча).
Проведем сравнительный анализ алгоритмов, работающих в пространстве объекта и в пространстве изображения (табл. 1) [2, 3, 4].
Алгоритмы, работающие в пространстве объекта | Алгоритмы, работающие в пространстве изображения | |
Система координат | Алгоритмы имеют дело с физической системой координат, в которой описываются данные объекты | Алгоритмы работают с системой координат экрана, на который визуализируются объекты |
Точность | Высокая точность (точные результаты, которые могут быть ограничены только точностью вычислений) | На точность вычислений влияет разрешающая способность экрана |
Объем вычислений | растет теоретически, как квадрат числа объектов n2 | растет теоретически, как nN, где n- количество объектов в сцене,N — число пикселов |
Трудоемкость | меньше | больше |
Эффективность | менее | более |
Однако, стоит отметить, что, не смотря достаточно большое количество разнотипных алгоритмов, в решении задачи загораживания существует ряд важных и до сих пор еще не решенных проблем:
- не существует универсального алгоритма, который не ограничивался бы определенным классом линий или поверхностей, необходимых для отображения объектов;
- практически невозможно выделить наилучший алгоритм, который был бы пригоден для всех типов графических устройств и любых приложений [4, 5].
Поэтому создание единого алгоритма, который смог бы справиться с удалением невидимых линий и поверхностей, является актуальной задачей повышенной сложности, которая не нашла еще своего решения.
В данной статье будет проведен сравнительный анализ двух алгоритмов удаления невидимых линий и поверхностей, работающих в пространстве изображения: алгоритма Коэна-Сазерленда и алгоритма Варнока.
Алгоритм Коэна-Сазерленда
Алгоритм Коэна-Сазерленда позволяет определить часть отрезка, пересекающую выделенную прямоугольную область, определяя таким образом видимость и невидимость отрезков. Суть алгоритма заключается в том, что плоскость разбивается на 9 частей прямыми, образующими стороны прямоугольника (рис. 1). Каждая часть имеет свой 4х-битный код. [6]
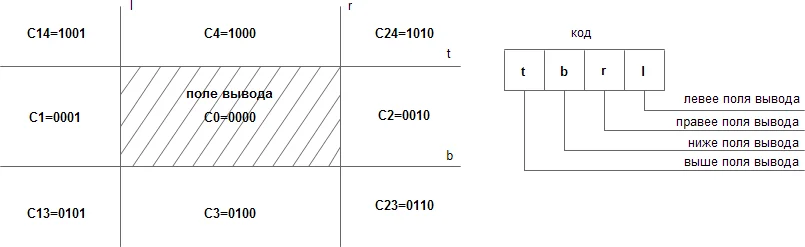
Поле вывода (с учетом границ) состоит из точек (x,y), которые удовлетворяют соотношения xl≤x≤xr и yb≤y≤yt . Допустим, что отрезок задан с помощью координат концевых точек (x1,y1) и (x2,y2). В начале алгоритма Коэна-Сазерленда выявляются полностью видимые и невидимые отрезки:
- Отрезок полностью принадлежит полю вывода, если его концы удовлетворяют условиям (xl≤x1≤xr, yb≤y1≤yt и xl≤x2≤xr, yb≤y2≤yt);
- Отрезок является полностью невидимым, если его оба конца лежат:.
- справа от ребра r (x1>xr, x2>xr);
- слева от ребра l (x1l, x2l);
- снизу от ребра b (y1b, y2b);
- сверху от ребра t (y1>yt, y2>yt).
В остальных случаях отрезок может (но не обязан) пересекать поле вывода.
В данном алгоритме каждой концевой точке отрезка присваивается свой код, в зависимости от ее расположения относительно поля вывода. Если коды концов отрезков равны нулю, то он (отрезок) лежит в поле вывода (внутри окна). Для анализа остальных случаев необходимо воспользоваться операцией логического умножения кодов [6, 7].
Руководствуясь полученной таблицей истинности, можно утверждать: если произведение концов отрезка принимает значение T (true), то этот отрезок полностью лежит по одну сторону одной из прямых (l, r, t или b), причем, важно отметить, он лежит во внешней стороне относительно поля вывода, следовательно, он полностью невидим. Если же произведение оказалось F(false), то отрезок частично находится в поле вывода [7].
Приведем общую блок-схему алгоритма Коэна-Сазерленда (рис. 2).
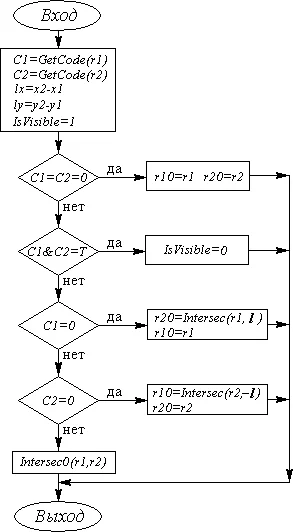
В блок-схеме используются следующие обозначения:
- GetCode(r) — вспомогательная функция, определения кода точки;
- C1, C2 — коды точек r1, r2;
- Intersec(r1,l), Intersec0(r1,l) — вспомогательные функции, поиска пересечения отрезка со сторонами окна при условии, что точка r1 лежит в окне и что обе точки лежат вне окна; если пересечения нет, устанавливает переменную IsVisible в 0, соответственно.
Входными данными являются точки (1), массив координат окна
(2).
На выходе получаем новые концевые точки , (3), а также значение переменной IsVisible (0 — отрезок видимый)[4].
Теперь приведем блок-схемы и рассмотрим более подробно вспомогательные функции: Intersec(r1,l) и Intersec0(r1,l) (рис. 3, 4).
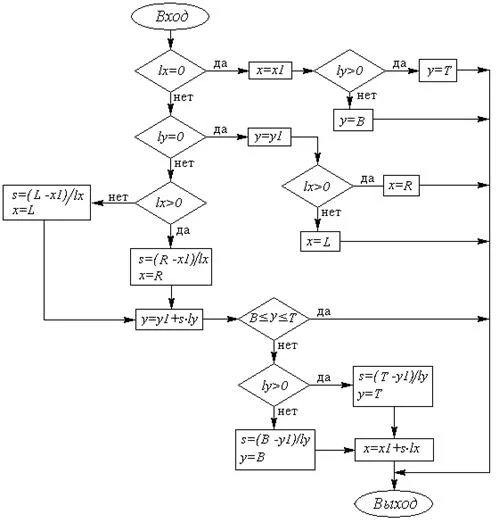
Воспользуемся методом поиска пересечений, использующим параметрическое уравнение прямой, проходящей через точки:
(4),
или в координатном виде:
, , , (5).
Определим точку пересечения отрезка с верхней границей окна, которая описывается соотношениями: (6).
Тогда условие пересечения границы и отрезка имеет вид:
(7).
Аналогично запишутся формулы для оставшихся границ окна. Если точка расположена внутри поля вывода, то, в зависимости от знака ly, необходимо искать пересечение либо с верхней, либо с нижней границей поля вывода (окна). Если такие пересечения отсутствуют, необходимо искать пересечения с двумя другими гранями окна (левой и правой стороной). До того как рассматривать выше описанные варианты, необходимо исключить случаи горизонтальных ly = 0 (пересечение с правой или левой границей: (L,y1), (R,y1), в зависимости от знака lx и вертикальных lx = 0 (пересечение с верхней или нижней границей: (x1,B), (x1,T) направлений отрезка.[7, 8]

Для случая, когда оба конца отрезка лежат вне окна вывода, в начале найдем одну точку пересечения с границей окна и заменим ею один из концов отрезка, а далее будем использовать вышеописанный алгоритм нахождения второй точки. Важно отметить, что первый шаг не в 100% случаев оканчивается успешно, так как с помощью предварительного анализа невозможно исключить все возможные невидимые отрезки. Аналогично предыдущему алгоритму перед поиском точек пересечения с полем вывода выполняется проверка на вертикальное и горизонтальное направление отрезка. Так как часть отрезков была исключена благодаря предварительному анализу, остаются только две возможные ситуации (рис. 5).
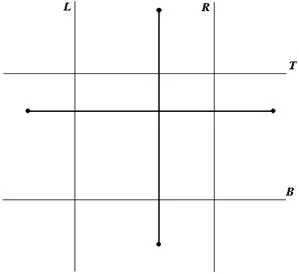
Точки пересечения на рисунке 6 определяются очевидным образом.
Далее последовательно рассматриваются 4 случая расположения точки относительно прямых, которые ограничивают поле вывода. При нахождении точки пересечения в любом из вариантов, процесс анализа останавливается, данная точка заменяется новой точкой и вызывается функция Intersec. Если при переборе всех 4х вариантов положительный ответ не был получен, переменная IsVisible получает значение 0.
Реализация алгоритма Коэна-Сазерленда для трехмерного случая аналогична двумерной реализации, за исключением того, что четырехразрядный код заменяется шестиразрядным (добавляются два бита глубины), следовательно, рассматриваются не прямоугольники, а параллелепипеды.
Алгоритм Варнока
Алгоритм Варнока работает в пространстве изображения. В процессе его работы так же рассматривается окно и определяется пустое ли оно или его содержимое просто для визуализации. Если эти два условия не выполняются, то происходит разбиение окна до тех пор, пока содержимое фрагментов окна не станет достаточно простым для визуализации или их размеры не достигнут пределов разрешения (в этом случае информация усредняется, т.е. выводится на экран с одинаковой интенсивностью или цветом)[9].
Существует множество видов алгоритма Варнока, все они различаются методами разбиения окна и критериями, определяющими является ли изображение в окне простым. Простейшая и оригинальная версия алгоритма Варнока выглядит следующим образом: окно, содержимое которого сложно визуализировать, разбивается на четыре одинаковых фрагмента, так называемых подокна; затем подокно, в котором есть содержимое, разбивается до тех пор, пока не будет достигнут предел разрешения экрана[8, 9].
Такой процесс разбиения можно изобразить в виде дерева. Важно отметить, что именно в алгоритме Варнока впервые была реализована структура данных, названная кватернарным деревом. Корень этого дерева — визуализируемое окно; узла дерева — подокна (они изображаются в виде прямоугольников, которые хранят левую нижнюю координату угла подокна, а также длину его стороны). Подокна обрабатываются последовательно друг за другом слева направо на каждом уровне разбиения дерева. Перебором находится подокно, содержащее сложное изображение, которое необходимо разбить (такое подокно называется активным узлом); и все повторяется на новом уровне. На каждом уровне есть активный узел, слева от активного узла располагаются пустые окна, справа от активного узла располагаются окна, которые будут обработаны позднее, т.е. будут объявлены пустыми или будут разбиты при обратном обходе дерева.
При помощи вышеописанного алгоритма можно удалить как невидимые линии, так и поверхности. Однако минусом данного способа является большое количество разбиений исходного окна, который возникает из-за простоты критерия разбиения и его негибкости. Эффективность повысится, если усложнить критерий и способ разбиения.
Чтобы рассматривать более сложные критерии разбиения окна необходимо сначала определить способы расположения многоугольника относительно окна.
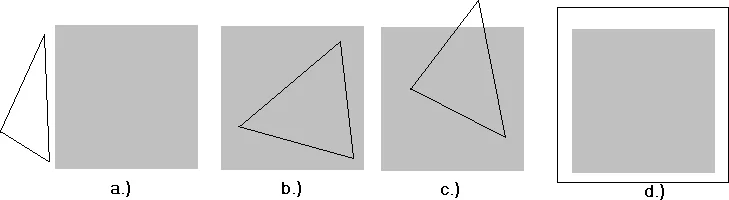
Будем выделять 4 разных многоугольника (рис. 6): внешний (расположен полностью вне окна); внутренний (полностью расположен внутри окна); пересекающий (пересекает хотя бы одну границу окна); охватывающий (окно целиком располагается внутри рассматриваемого прямоугольника) [2, 6].
Зная вышеописанные типы многоугольников, можно рассмотреть следующие правила обработки окна. Для каждого окна:
- если в сцене присутствуют только внешние многоугольники по отношению к окну, то это окно считается пустым; оно не разбивается и изображается с фоновой интенсивность или цветом;
- если в сцене присутствует лишь один многоугольник, который располагается внутри окна, то площадь вне многоугольника изображается с фоновой интенсивностью или цветом, а площадь внутри многоугольника, заполняется соответствующим ему цветом или интенсивностью;
- если в сцене располагается пересекающий многоугольник, то площадь вне многоугольника изображается с фоновой интенсивностью или цветом, а площадь внутри многоугольника, которая располагается внутри окна, заполняется соответствующим ему цветом или интенсивностью;
- если в сцене присутствует только один многоугольник (охватывающий), то окно изображается с интенсивностью или цветом соответствующими охватывающему многоугольнику;
- если в сцене присутствует хотя бы один охватывающий многоугольник, расположенный ближе других к точке наблюдения, то окно заполняется интенсивностью или цветом, соответствующими охватывающему многоугольнику.
В любом другом случае необходимо провести разбиение окна [1,6].
Последний пункт для обработки окна решает задачу удалений невидимых поверхностей. Получается, что многоугольник, расположенный ближе всего к наблюдателю (к точке наблюдения) перекрывает любые другие многоугольники. Остальные пункты для обработки окна позволяют сократить число подразбиений окна, так как в них рассматриваются ситуации пересечения окна и только одного многоугольника.
Для реализации данного алгоритма необходимо определить взаимное расположение многоугольника и окна с помощью функций, которые просты в реализации, если рассматриваются прямоугольные окна и выпуклые многоугольники, а в случае невыпуклых многоугольников задача становится сложнее.
Для сравнительного анализа выбранных алгоритмов были выделены следующие критерии: основная идея алгоритма, пространство в котором он работает, наличие возможности удаления невидимых линий и поверхностей, количество итераций, критерий завершения, эффективность для сложных сцен, способы повышения эффективности алгоритма, частота использования, сложность реализации и точность. Для наглядности результаты анализа были сведены в таблицу 2.
Алгоритм Коэна-Сазерленда | Алгоритм Варнока | |
Основная идея | Чтобы определить, как отрезок расположен относительно окна вывода, необходимо проверить коды концов отрезка и в зависимости от их значения сделать выводы. | Чтобы проанализировать является ли элемент изображения видимым или невидимым в окне вывода, необходимо осуществить последовательное разбиение объектного пространства на составные части. |
Пространство, в котором работает алгоритм | Работает в пространстве изображения | Работает в пространстве изображения |
Возможность удаления невидимых линий | есть | есть |
Возможность удаления невидимых поверхностей | нет | есть |
Количество итераций | выполняет отсечение за несколько итераций (около 2х) | прямо пропорционально насыщенности изображения |
Критерий завершения | Отсечение отрезков продолжается до тех пор, пока длина очередного отрезка не станет меньше наперед заданной точности. | Разбиение области стоит прекратить, как только ее размер станет не больше одного пикселя. |
Эффективность для сложных сцен | Низкая | Средняя |
Повышение эффективности алгоритма |
|
|
Частота использования | более | менее |
Сложность реализации | средняя |
|
Точность | ограничена разрешающей способностью экрана | |
На практике, сравнительный анализ алгоритма Коэна-Сазерленда и алгоритм Варнока (а также любых других алгоритмов удаления невидимых линий и поверхностей) крайне затруднителен. Так как в различных случаях при работе с различными моделями пространства будут эффективны различные алгоритмы. Даже при работе с одной и той же моделью в зависимости от точки расположения наблюдателя могут быть эффективны различные алгоритмы удаления невидимых линий и поверхностей.