Представленный ниже возможный вариант плана-конспекта урока № 25 для первого года графической подготовки школьников разработан в соответствии с опубликованными нами ранее тематическими планированиями уроков черчения [7 — 8]. При этом были использованы классические пособия учебно-методического комплекта (УМК) по черчению: программа, учебник, рабочая тетрадь, методическое пособие для учителя А.Д. Ботвинникова и его соавторов [1 — 6], а также другая учебно-методическая литература [9 — 23].
Теоретическая основа планирования учебной работы по черчению и подготовки учителя к уроку в развёрнутой форме нами была представлена в отдельной публикации [10]. Были даны образцы планов-конспектов уроков черчения №№ 1 — 6, 14 для первого года графической подготовки школьников [11 — 17]. В отдельном журнале также представлен пример плана-конспекта урока № 5 для второго года обучения школьников черчению с примером анализа предполагаемого или проведённого урока [18].
В учебнике черчения А.Д. Ботвинникова и др. вопросы деления отрезка и угла на равные части его авторами не рассмотрены, ссылаясь на то, что учащиеся эти построения изучали ранее на уроках геометрии и других предметов [2, с. 98-99]. В учебнике рассмотрены лишь деление окружности на равные части и сопряжения. Но мы в предлагаемом ниже плане-конспекте решили представить не только методику обучения школьников делению окружности на равные части, но и дать методику обучения учащихся способам деления отрезка и угла на равные части с использованием классического учебника С.К. Боголюбова [19], поскольку опыт работы в школе показал, что учащиеся зачастую не помнят, как выполнять эти геометрические построения.
План-конспект урока черчения № 25 (Первый год обучения)
Тема урока: Геометрические построения: деление отрезка, угла и окружности на равные части.
Цели урока
Образовательная
- Обучение школьников делению отрезка, угла и окружности на равные части с помощью чертёжных инструментов;
- Закрепить полученные знания школьников путём выполнения ими графический упражнений;
- Дальнейшее формирование умений и навыков работы школьников с чертёжными инструментами, учебными и справочными материалами в процессе их графической деятельности.
Воспитательная
- Формировать познавательный интерес учащихся к предмету;
- Содействовать воспитанию терпения, аккуратности, внимания, усидчивости, трудолюбия учащихся, необходимых им для качественного выполнения чертежей;
- Формировать навыки самостоятельной работы школьников во время выполнения ими упражнений;
- Способствовать эстетическому воспитанию школьников путём их обучения красивому расположению изображений на листе бумаги.
Развивающая
- Способствовать дальнейшему развитию глазомера, зрительной памяти и технической речи учащихся.
Учебные пособия, чертежные инструменты, принадлежности и материалы
Для учителя — учебник [2]; учебные таблицы и видеоматериалы, иллюстрирующие деление отрезка, угла и окружности на равные части; образец выполненной графической работы школьником по делению окружности на равные части на уроке вслед за учителем, показывающим построения на классной доске; набор дифференцированных карточек-заданий и варианты их решений; чертежные инструменты и мел для работы на доске.
Для учащихся — учебник [2], ученическая тетрадь, Рабочая тетрадь [3] чертежный лист формата А4 с рамкой и основной надписью, чертёжные инструменты и принадлежности.
Тип урока
Урок изучения нового материала.
Ход урока
1. Организационная часть — 2 мин.
- Приветствие;
- Выявление или назначение дежурных. Напоминание дежурным об их обязанностях;
- Проверка явки учащихся;
- Заполнение учителем классного журнала (можно в конце урока);
- Проверка готовности учащихся к уроку. Выдача учащимся недостающих учебных пособий, чертежных инструментов, принадлежностей и материалов из фонда кабинета для работы на данном занятии.
2. Сообщение темы, цели и задач урока; мотивация учебной деятельности школьников — 3 мин.
2.1. В левой верхней части классной доски учитель мелом заранее пишет чертёжным шрифтом дату проведения урока и его порядковый № 25. В средней верхней части доски указывает тему урока «Геометрические построения: деление отрезка, угла, и окружности на равные части». В правом верхнем углу доски указывает домашнее задание: Повторить § 15.2; тем, кто не успел выполнить классную работу и графическое задание на уроке, дочертить их дома и сдать работы учителю на проверку на следующем уроке.
Обращая внимание учащихся на доску, учитель вслух проговаривает написанное и просит учеников записать полученную информацию в ученических тетрадях.
2.2. Далее учитель ставит перед школьниками цели и задачи урока:
- Научиться правильному делению отрезка, угла и окружности на равные части с помощью чертёжных инструментов;
- Закрепить полученные знания на данном уроке путём выполнения графического упражнения;
- Продолжить: 1) формирование умений и навыков работы с чертёжными инструментами, учебными и справочными материалами в процессе графической деятельности; 2) развитие глазомера, зрительной памяти и технической речи.
2.3. Мотивируя учебную деятельность школьников, учитель сообщает, что материалы данного урока им пригодятся во взрослой жизни при работе, связанной с чертёжно-графической документацией, например, в конструкторских бюро и цехах на машиностроительных заводах и т.д., а в школе — при дальнейшем изучении черчения, в частности, при выполнении различных графических изображений на чертёжных листах, в ученических и Рабочих тетрадях. Кроме того, полученные знания и умения на данном уроке многим из них пригодятся на занятиях по инженерной графике в технических учебных заведениях, куда они могут поступить на дальнейшую учёбу после окончания общеобразовательного учреждения.
Для большей наглядности в процессе мотивации учебной деятельности школьников учителю необходимо продемонстрировать им фотографии технических деталей и их чертежи, выполненные с использованием деления отрезка, угла и окружности на равные части (рис. 1-4; 6-10). Кроме того, демонстрируя рис. 1, школьникам учитель сообщает, что изучаемые на данном уроке геометрические построения широко используются не только при выполнении чертежей и рисунков технических деталей, но и изделий художественно-прикладного искусства с узорами, орнаментами на кружевах, вышивкой, резьбой по дереву и металлу и т.п., продуктов графического дизайна (логотипы, товарные знаки, различные символы), в архитектуре и т.д. [21, с. 30].
В качестве дополнительной мотивации учебной деятельности школьников учитель также сообщает им о том, что графические работы, выполненные ими на этом уроке, будут оценены, а оценки — выставлены в журнал.
![</em> Примеры использования простейших геометрических построений в технике, дизайне, прикладном искусстве [20, с. 29, <em>рис. 2.31</em>; 21, с. 30<em>, рис. 2.28</em>]](/res/quz94mhffz.webp)
3. Объяснение нового материала — 20 мин.
3.1. Демонстрируя рис. 2 на большом экране, учитель с помощью чертёжных инструментов последовательно показывает школьникам на классной доске деление отрезка прямой на две и четыре равные части. При этом он им сообщает, что из концов отрезка AB циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 2, а). Точки m и n соединяют прямой, которая пересекает отрезок AB в точке C. Точка C делит отрезок AB на две равные части. Проделав подобное построение для отрезка AC, находим его середину — точку D. Повторив построение для отрезка CB, разделим отрезок AB на четыре равные части [19, с. 27]. Школьники вслед за учителем выполняют эти и последующие геометрические построения в своих ученических тетрадях.
Учащимся сообщается, что при вычерчивании детали, показанной на рис. 2, б, применяется способ деления отрезка на четыре части.
![</em>Деление отрезка прямой на две и четыре равные части: а — деление отрезка на две равные части; б — чертёж детали, выполненный с применением способа деления отрезка на четыре равные части [19, с. 27, <em>рис. 43</em>]](/res/3rkwivzune.webp)
![</em> Деление отрезка на любое число равных частей с помощью угольника и линейки: а — деление отрезка на одиннадцать равных частей; б — чертёж детали c десятью отверстиями, выполненный с применением способа деления отрезка L на девять равных частей [19, с. 28, <em>рис. 44</em>]](/res/nj3qfk8r12.webp)
3.2. Деление отрезка прямой на любое число равных частей. Учитель на экран проецирует изображения, представленные на рис. 3. Затем он на классной доске с помощью инструментов показывает способ деления отрезка AB на 11 равных частей. Школьники узнают, что для этого из любого конца данного отрезка, например, из точки B (рис. 3, а), проводят под произвольным острым углом вспомогательную прямую линию BC, на которой от точки B измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой A прямой AB. Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой 11A, которые и разделяют отрезок AB на 11 равных частей.
На рис. 3, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части [19, с. 27-28].
3.3. Учитель обращает внимание школьников на рис. 4, затем начинает объяснять и показывать на классной доске способы деления угла на две и четыре равные части. Так же, как и в предыдущих случаях, каждый школьник выполняет очередные геометрические построения в своей тетради вслед за учителем, объясняющим учебный материал. Используя рис. 4, а и слушая объяснение учителя, школьники в тетради из вершины угла проводят произвольным радиусом дугу до пересечения со сторонами угла BAC в точках n и k. Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги nk, до взаимного пересечения в точке m. Вершину угла соединяют с точкой m прямой, которая делит угол BAC пополам. Эта прямая называется биссектрисой угла BAC. Повторяя это построение с полученными углами BAm и mAC угол BAC можно разделить на четыре равные части и т. д. [19, с. 29].
![</em>Деление углов на равные части: а — деление угла на две и четыре равные части; б — деление прямого угла на три равные части [19, с. 29, <em>рис. 47</em>]](/res/b2oqtewwoy.webp)
3.4. Изучая способ деления прямого угла на три равные части, школьники из вершины А прямого угла (рис. 4, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b, из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла A прямыми и получают стороны Am и An углов BAm и nAC, равных 1/3 прямого угла, т. е. 30°. Школьникам учитель сообщает, что если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол ABC можно разделить на три равные части угольником с углами 30 и 60° [19, с. 29, рис. 48, а]. При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° [19, с. 29, рис. 48, б].
![</em> Образец графической работы школьника по делению окружностей на равные части, выполненной им в ходе изучения темы урока с использованием учебника черчения А.Д. Ботвинникова и др. [2, с. 100 — 102, рис. 124 — 129]](/res/5vg7puufpj.webp)
3.5. На данном этапе урока учитель начинает обучать учащихся делению окружности на равные части. С этой целью им предлагается найти рис. 124 — 129 на с. 100 — 102 традиционного школьного учебника «Черчение» [2], рассмотреть их и опираясь на учебную таблицу «Образец графической работы школьников по делению окружностей на равные части» (рис. 5), композиционно правильно наметить центры и начертить циркулем восемь окружностей Ø 40 мм сплошной тонкой линией на чертёжном листе бумаги формата А4 или в ученической тетради. Затем вслед за учителем, объясняющим и показывающим деление окружности на равные части на классной доске с помощью чертёжных инструментов, ребята начинают выполнять геометрические построения — делить окружности на равные части так, как показано на рис. 5.
3.5.1. В верхней части листа бумаги (рис. 5) школьники показывают деление окружности на четыре и восемь равных частей с использованием рис.6. На рис.6, а показана крышка, в которой имеется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 6, г) учащимся необходимо разделить окружность на восемь равных частей. Это им можно сделать с помощью угольника с углами 45° (рис. 6, в), гипотенуза угольника должна проходить через центр окружности, или построением.
![</em>: Фото технической детали «Крышка» с восемью равномерно расположенными отверстиями по окружности (а); деление окружности на 4 и 8 равных частей с помощью циркуля (б), угольника и линейки (в); чертёж контура крышки (г) [19, с. 32, <em>рис. 52</em>]](/res/cul8yvuhzs.webp)
В процессе изучения учебного материала, учащиеся также узнают, что два взаимно перпендикулярных диаметра окружности делят ее на четыре равные части (точки 1, 3, 5, 7 на рис. 6, б). Далее учитель ребятам объясняет, чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8 на рис. 6, б [19, с.31-32].
3.5.2. Деление окружности на три, шесть и двенадцать равных частей учащиеся размещают в средней части и в левом нижнем углу листа бумаги формата А4 (рис. 5). Во фланце (рис. 7, а) имеется три отверстия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 7, г) нужно разделить окружность на три равные части.
![</em>: Фото технической детали «Фланец» с тремя равномерно расположенными отверстиями по окружности (а); деление окружности на три равные части с помощью циркуля (б), угольника и линейки (в); чертёж контура фланца (г) [19, с. 32, <em>рис. 53</em>]](/res/xkkrxftrfz.webp)
Учитель ребятам объясняет, что для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из любой точки окружности, например, точки A, провести дугу радиусом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки A, с окружностью (рис. 7, б).
Школьникам сообщается, что разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 7, в), гипотенуза угольника должна проходить через центр окружности [19, с. 31 — 32, 34].
Школьники на уроке узнают, что на рис. 8, б показано деление окружности циркулем на шесть равных частей. В этом случае выполняется то же построение, что на рис. 7, б, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом R, равным радиусу окружности.
![</em>: Фото технической детали «Крышка» с шестью равномерно расположенными отверстиями по окружности (а); деление окружности на шесть равных частей с помощью циркуля (б), угольника и линейки (в); чертёж контура крышки (г) [19, с. 32, 34, <em>рис. 54</em>]](/res/ixhb6r5ddc.webp)
Учащиеся убеждаются в том, что разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 8, в). На рис. 8, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.
Чтобы выполнить чертеж детали (рис. 9, а), которая имеет 12 отверстий, равномерно расположенных по окружностям, нужно разделить осевую окружность на 12 равных частей (рис. 9, г) [19, с. 31 — 32, 34].
![</em>: Фото технической детали с двенадцатью равномерно расположенными отверстиями по окружности (а); деление окружности на двенадцать равных частей с помощью циркуля (б), угольника и линейки (в); чертёж контура детали (г) [19, с. 32, <em>рис. 55</em>]](/res/wmizuk03gg.webp)
Ребята сами догадываются о том, что при делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 8, б), но дуги радиусом R описывать четыре раза из точек 1,7, 4 и 10 (рис. 9, б).
Ребята познают, что, используя угольник с углами 30 и 60° с последующим поворотом его на 180°, делят окружность на 12 равных частей (рис. 9, в) [19, с. 31 — 32, 34].
3.5.3. В правом нижнем углу чертёжного листа формата А4 (рис. 5) школьники на уроке показывают деление окружности на пять равных частей вслед за учителем, объясняющим и показывающим графические операции с помощью чертёжных инструментов на классной доске. В плашке (рис. 10, а) имеется пять отверстий, равномерно расположенных по окружности. Выполняя чертеж плашки (рис. 10, в), необходимо разделить окружность на пять равных частей. Через намеченный центр O (рис. 10, б) при помощи рейсшины и угольника проводят осевые линии и из точки O циркулем описывают окружность заданного диаметра. Из точки A радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку C. Из точки C радиусом R1, равным расстоянию от точки C до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке m. Из точки 1 радиусом R2, равным расстоянию от точки 1 до точки m, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3, 4 и 5 находят, откладывая циркулем отрезки, равные m1.
![</em>: Фото технической детали «Плашка» с пятью равномерно расположенными отверстиями по окружности (а); деление окружности на пять равных частей с помощью циркуля (б); чертёж контура плашки (в) [19, с. 33, <em>рис. 56</em>]](/res/wzrwzm9p6f.webp)
Здесь важно обратить внимание школьников ещё на один способ деления окружности на пять равных частей (рис. 5, нижнее правое изображение). Кроме того, школьникам необходимо предложить найти рис. 129 на с. 102 в учебнике черчения [2]. Авторы учебника пишут, что пятой части окружности соответствует центральный угол в 72° (360°:5=72°). Этот угол можно построить при помощи транспортира. Полученную при этом хорду окружности откладывают раствором циркуля по длине заданной окружности так, как показано на рис. 5 в нижнем правом углу и на рис. 129 (с. 102) в учебнике.
4. Обобщение и закрепление знаний; выполнение графического задания — 15 мин.
4.1. С целью закрепления изученного материала учитель предлагает школьникам устно ответить на следующие вопросы:
- При помощи каких чертёжных инструментов следует делить окружности на равные части? (При помощи линейки, угольников с различными углами, циркуля и транспортира).
- Какой угол делят на три равные части с помощью циркуля? (Прямой угол);
- Чему равен раствор циркуля при делении окружности на три равные части и на шесть равных частей? (Радиусу заданной окружности).
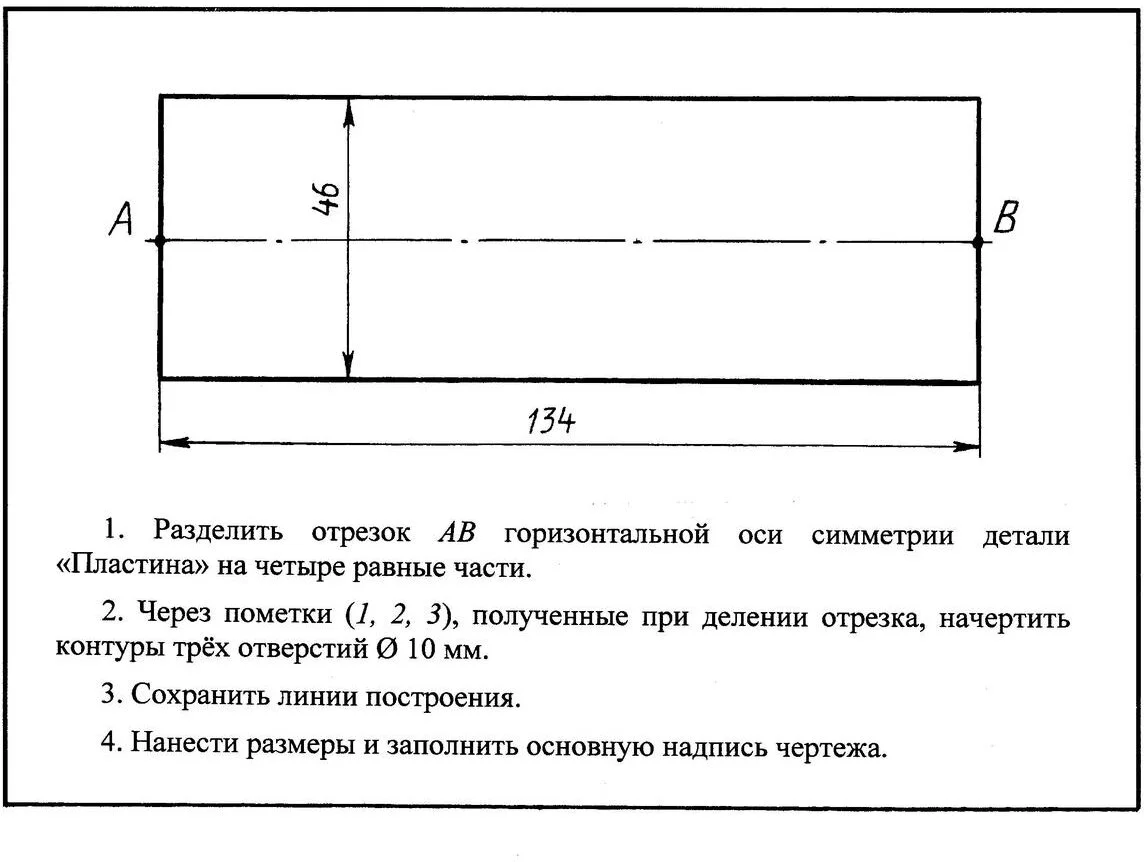
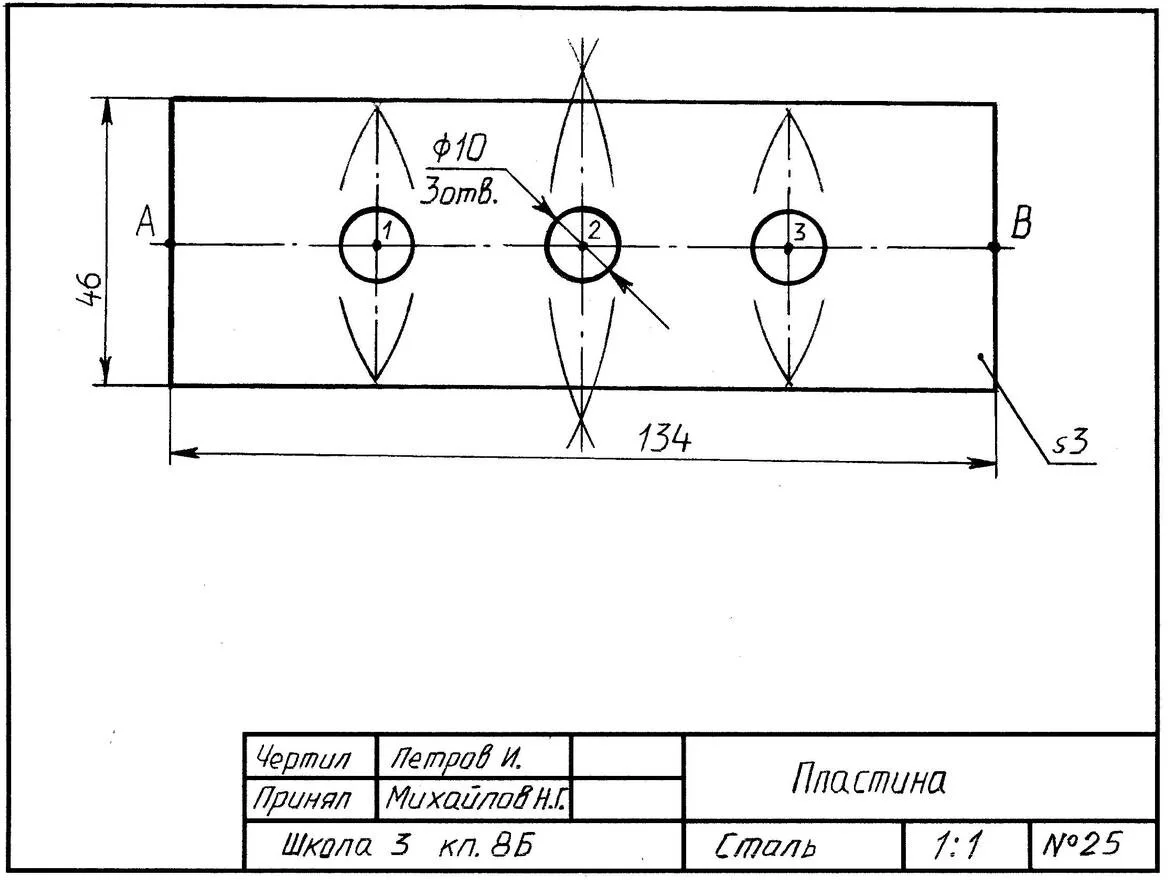
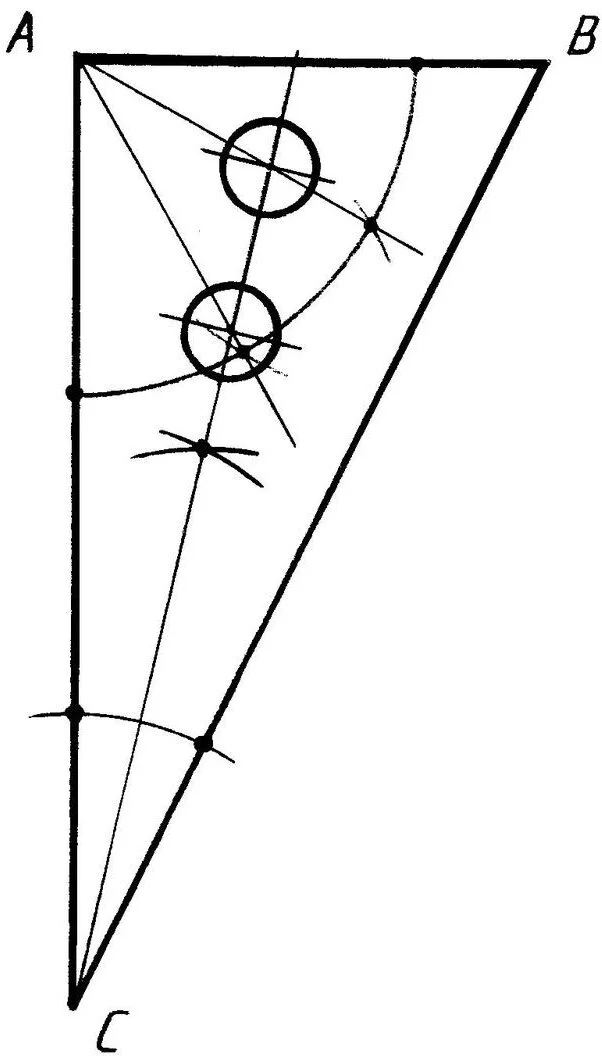
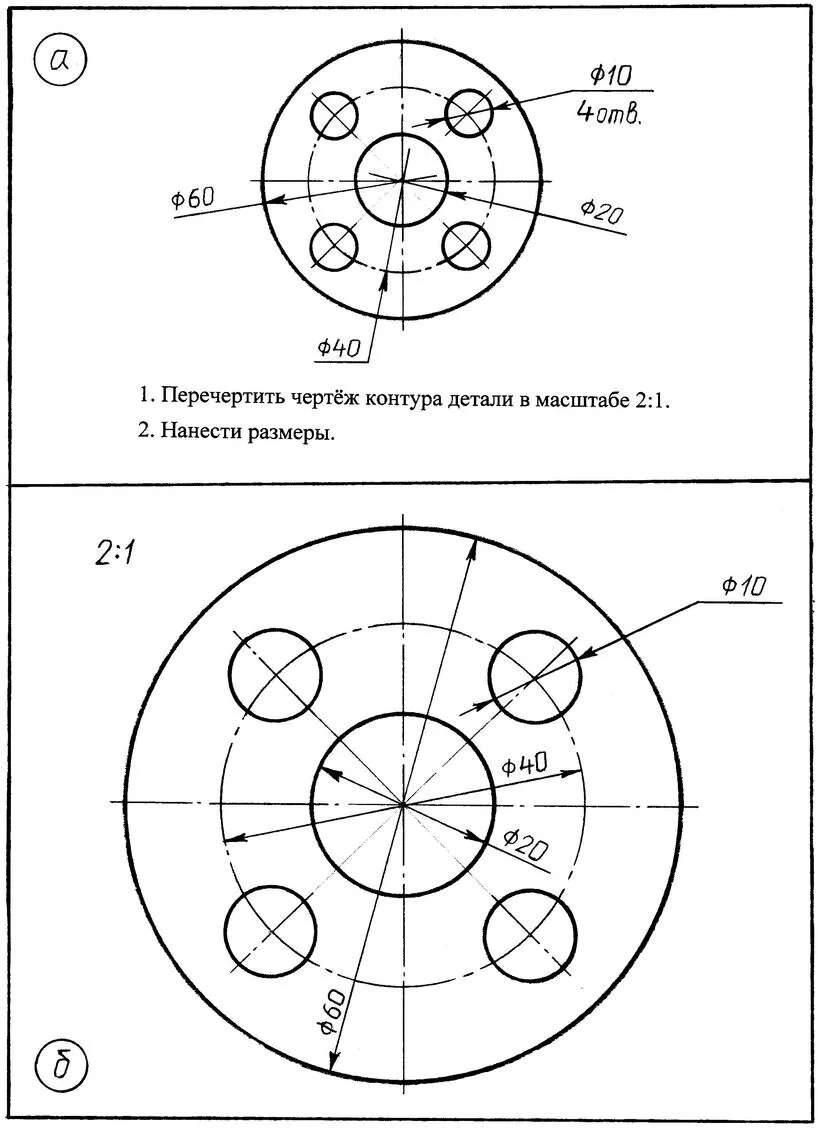
4.2. На втором этапе закрепления изученного материала школьникам предлагается выполнить одно задание из трёх предложенных учителем заданий (рис. 11; 13; 15, а). Предполагаемые образцы выполненных заданий школьниками даны на рис. 12; 14; 15, б).
5. Задание на дом — 1 мин.
Повторить § 15.2. Тем, кто не успел выполнить классную работу и графическое задание на уроке, дочертить их дома и сдать работы учителю на проверку на следующем уроке.

6. Подведение итогов урока — 4 мин.:
- учитель просит назвать школьников сложности, с которыми они встретились на уроке, затем дает общую характеристику их учебной деятельности на уроке; при этом сообщает им о достижении целей урока, выявленных недостатках и путях их устранения;
- объективно оценивает результаты коллективного и индивидуального труда; выставляет отметки в классный журнал и в дневники учащихся;
- предлагает тем, кто не успел закончить работу на уроке, доделать её дома и принести на следующий урок;
- напоминает дежурным об их обязанностях: после звонка с урока остаться и прибраться в классе, оказать учителю другую необходимую помощь;
- благодарит учащихся за учебно-познавательную деятельность и заканчивает урок.