На данном этапе прогнозирование является основой финансового планирования многих фирм и компаний, касается задач управления, оптимизации и многих других. Этим и объясняется актуальность рассматриваемой темы — задача определения будущих значений является неотъемлемой частью ежедневной работы большого числа организаций.
Существует множество моделей и методов прогнозирования будущих значений временного ряда: регрессионные модели, трендовые модели, нейросетевые модели, модели на базе цепей Маркова и т.д. Подробнее о них можно узнать в работах [1], [3], [4].
В данной статье рассматриваются модели тренда и множественной регрессии и предложен новый подход к задаче прогнозирования.
Задача множественной регрессии основана на предположении, что временной ряд, предложенный для построения прогноза, является зависимой переменной, на которую оказывают влияние независимые переменные — внешние факторы, влияние которых определяется, например, экономическими связями между переменными. Ознакомиться с классической задачей парной и множественной регрессии можно в [2].
При решении задачи в отсутствии внешних факторов временной ряд можно представить в качестве тренда. Такие модели позволяют строить долгосрочные прогнозы на основе значений конкретного ряда. Чаще всего трендовые модели представлены нелинейными уравнениями, поэтому выделяют полиномиальный, экспоненциальный, логарифмический, степенной и др. тренды. Подробнее классические задачи прогнозирования на основе трендовых моделей указаны в [5]. С помощью значений некоторых числовых характеристик (дисперсии, индекса детерминации) определяется модель, наилучшим образом приближающая временной ряд и позволяющая построить адекватный прогноз будущих значений.
Дальнейшее знакомство с данной статьей возможно при условии ознакомления с указанными выше моделями и методами.
При рассмотрении множественной регрессии зависимая и независимые переменные представляют собой временные ряды. В отдельности эти временные ряды могут обладать свойствами каких-либо трендовых моделей. Главная идея состоит в том, чтобы рассматривать смешанную регрессионно-трендовую модель. При этом возможны несколько способов построения модели. Пусть в нашем случае в качестве тренда рассматривается только зависимая переменная. Рассмотрим основные шаги построения модели.
На первом шаге рассматривается зависимая переменная y(t) в отдельности. Необходимо подобрать адекватную трендовую модель, построить временной ряд выравненных значений и найти отклонения значений полученного ряда от исходного. Данный временной ряд, состоящий из отклонений, будет являться зависимой переменной на следующем шаге.
На втором шаге рассматривается регрессионная модель, в которой в качестве матрицы А выступают независимые переменные, а в качестве прогнозируемой — ряд, полученный на предыдущем шаге. Далее строится прогноз x(t) для этого временного ряда, который на данном этапе не является решением задачи.
Для построения прогноза исходного временного ряда на третьем шаге необходимо вернуться к трендовой модели и построить прогноз, используя ряд, полученный на втором шаге. Для этого к прогнозному значению тренда необходимо прибавить значения ряда x(t).
После описание смешанного метода можно переходить к практическим результатам.
Пусть дан некоторый временной ряд. Построим его прогноз на основе регрессионной модели, модели тренда и смешанной модели и сравним полученные результаты. Данный по условию ряд тестовый, поэтому имеются его фактические будущие значения, что позволит адекватно оценить метод прогнозирования.
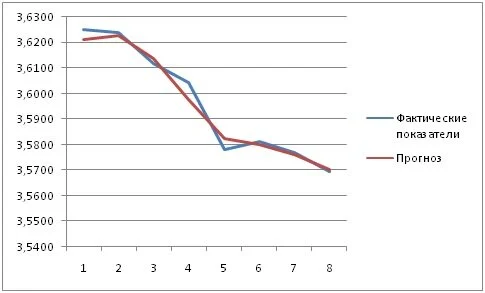
На рисунке 1 представлены результаты прогнозирования на основе множественной регрессии. В данном случае прогноз достаточно близок к фактическим будущим значениям переменной.
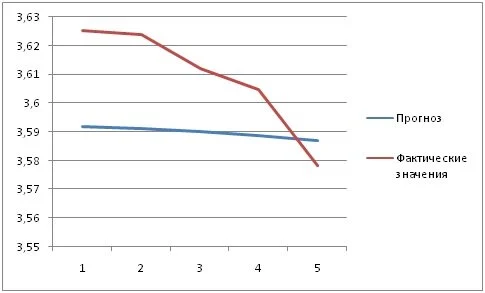
На рисунке 2 задача прогнозирования для того же самого временного ряда решена на основе предположения соответствия ряда некоторой трендовой модели. В данном случае рассматривались четыре трендовых модели (линейная, полиномиальная второй степени, экспоненциальная и степенная). Индекс детерминации оказался выше у полиномиальной модели. По графику видно, что прогнозные значения значительно отстоят от фактических.
Результаты прогнозирования на основе смешанной модели представлены на рисунке 3.
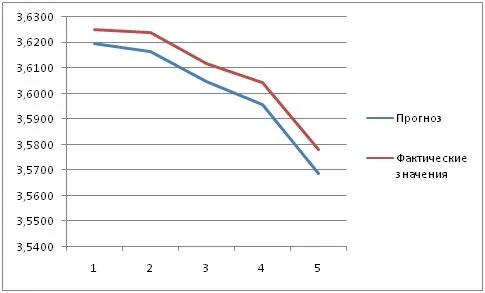
Данные результаты позволяют сделать вывод о том, что смешанная модель действительно позволяет строить прогноз, наилучшим образом приближающийся к решению.
Стоит отметить, что модель действительно работает только в том случае, когда зависимая переменная ведёт себя как некоторый тренд, причём этот тренд правильно определён на первом шаге. Поэтому как бы хороша ни была модель прогнозирования, она не может адекватно отражать все возможные ситуация. Для каждого случая необходимо своя модель. Выбор модели прогнозирования основывается на числовых характеристиках модели временного ряда, отношениями между переменными, что выражает предметная область рассматриваемого явления, а также от личного опыта специалиста, занимающегося задачами прогнозирования.