В период 1988-2014 гг. появилось достаточно большое количество работ, посвященных изучению фракталов и фрактальных объектов [1, 2, 5-27], в них приведено большое количество фракталов, полученных с помощью компьютерных расчетов.
В окружающей нас природе фрактальные структуры с той или иной степенью подобности можно встретить практически повсеместно. Очевидно, отчасти это связано с тем, что многие органические и неорганические формы формируются аналогично.
К фрактально подобным объектам можно отнести облака, электрический разряд в воздухе, морские раковины, кроны деревьев, кровеносную и дыхательную системы, границы морских побережий, горные цепи, зимние узоры на стекле, трещины в некоторых породах, и т.д., — по сути, список можно продолжать до бесконечности [1, 3, 4, 6, 10, 22].
Рассмотрим, например, отдельную веточку дерева. Внимательное ее изучение обязательно натолкнет на мысль, что она со своими сучками и развилками очень похожа на дерево. Такая схожесть отдельной части (ветки) с целым (деревом) говорит в пользу распространенного в природе принципа рекурсивного самоподобия. Поэтому разнообразные природные формы можно описать фрактальным алгоритмом.
Согласно [17], фрактальное множество обладает следующими основными свойствами:
- имеет тонкую структуру, (содержит произвольно малые масштабы);
- слишком нерегулярно, чтобы быть описанным на традиционном языке геометрии;
- имеет некоторую форму самоподобия, включая приближенную или статистическую;
- как правило, фрактальная размерность больше топологической;
- в большинстве интересных случаев определяется очень просто, например, рекурсивно.
В рамках одной из нескольких существующих классификаций фракталов выделяют геометрические, алгебраические и стохастические фракталы.
Геометрические фракталы
Это самый первый, ранний тип фракталов, с которых, по сути, и началась история фракталов. Такие фракталы — одни из самых наглядных, в них сразу видна самоподобность частей, и получаются они путем простых геометрических построений:
- Задается фигура (нулевое поколение), на основе которой будет строиться фрактал;
- Задается процедура-генератор, которая на основе определенного правила (или правил) преобразует нулевое поколение;
- Бесконечное повторение процедуры-генератора позволяет получить геометрический фрактал.
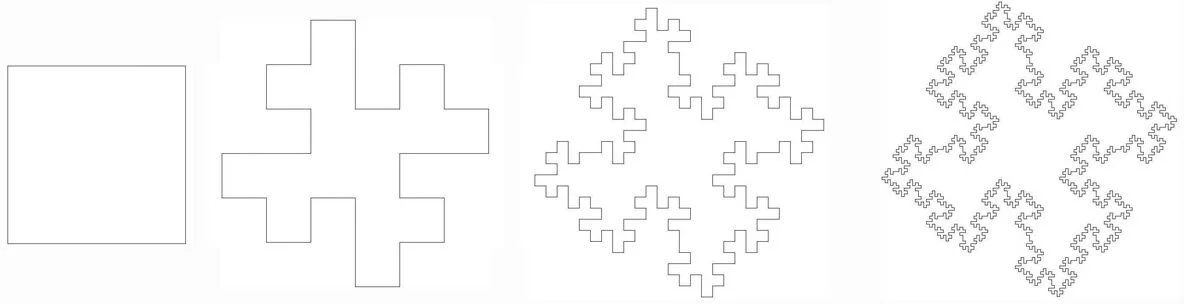
К геометрическим фракталам относятся: треугольник Серпинского (рис. 1 и 2), ковер Серпинского (рис. 3), кривая Коха, снежинка Коха, квадратная кривая Коха (рис. 4), кривая Пеано, пыль Кантора, губка Менгера (рис. 5), дракон Хартера-Хайтвея [10] (рис. 6), L-системы, и др.
Рассмотрим правила построения некоторых перечисленных фракталов.

Фрактал «треугольник Серпинского» был получен в 1915 г. польским математиком Вацлавом Серпинским. Для его получения используется равносторонний треугольник. На первом этапе построения необходимо разделить этот треугольник средними линиями на 4 треугольника, и изъять внутренний из них. После этого эти же действия повторить с каждым из оставшихся трех треугольников, и т.д. (см. рис. 1). Треугольник Серпинского имеет нулевую площадь.
Стоит отметить, что существует еще несколько способов построения треугольника Серпинского, один из которых использует случайное блуждание точки на плоскости. Рис. 2 получен как раз таким способом, при построении использовано точек.

Фрактал «ковер Серпинского» был описан В. Серпинским в 1915 г., он представляет собой квадрат, который делится двумя горизонтальными и двумя вертикальными линиями на девять равных частей-квадратов, подобных исходному. Затем центральный квадрат выбрасывается, а к остальным восьми применяется та же процедура, и т.д. (рис. 3). Ковер Серпинского имеет нулевую площадь.

Губка Менгера (рис. 5) представляет собой обобщение ковра Серпинского на трехмерное пространство. Объем губки равен нулю, но она имеет бесконечно большую площадь.


Такое понятие, как L-системы появилось в 1968 году благодаря датскому математику и биологу Аристриду Линденмайеру. Изначально они использовались при изучении формальных языков и в биологических моделях селекции. L-системы позволяют строить разнообразные самоподобные фракталы, включая ковер Серпинского и снежинку Коха [5, 27].
Несколько позже L-системы стали использовать для генерации растительных форм, таких как листья, кусты и деревья (в большинстве компьютерных игр растения ландшафтов генерируются именно L-системами).
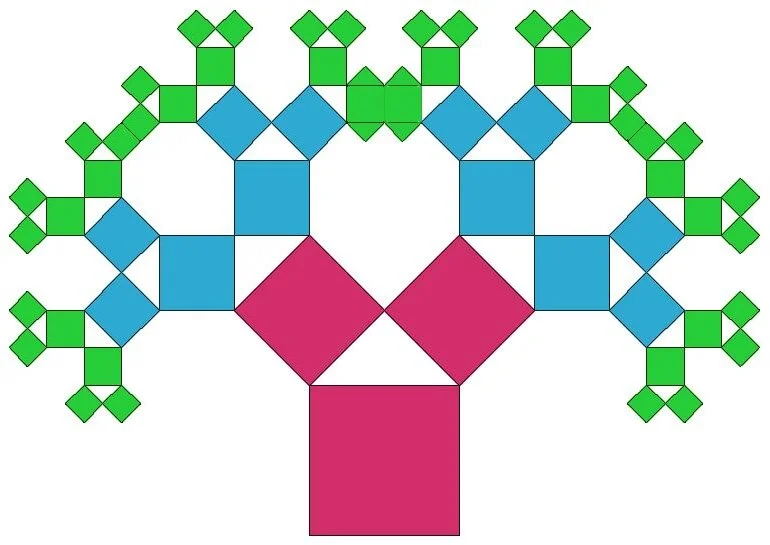
Ниже на рис. 7 приведен фрактал «Дерево Пифагора», построенный L-системой. Название связано с тем, что каждая тройка попарно соприкасающихся квадратов ограничивает прямоугольный треугольник. Для большего эффекта квадраты на изображении закрашены разными цветами согласно номерам итераций.
На рис. 8 приведены некоторые примеры, демонстрирующие работу L-систем и моделирующие некоторые растительные формы; изображения получены в программе Graphic x4.2007.
Геометрические фракталы в компьютерной графике используются для получения изображений листьев, кустов, деревьев, береговых линий, объемных текстур, и т. д.

Построение конструктивных фракталов возможно также с помощью системы итерируемых функций (Iterated Function System), или сокращенно IFS, представляющих собой систему функций некоторого фиксированного класса, позволяющих отображать одно многомерное множество на другое. Одна из самых простых IFS включает аффинные преобразования плоскости, и в двумерном пространстве задается на основе 6 коэффициентов:
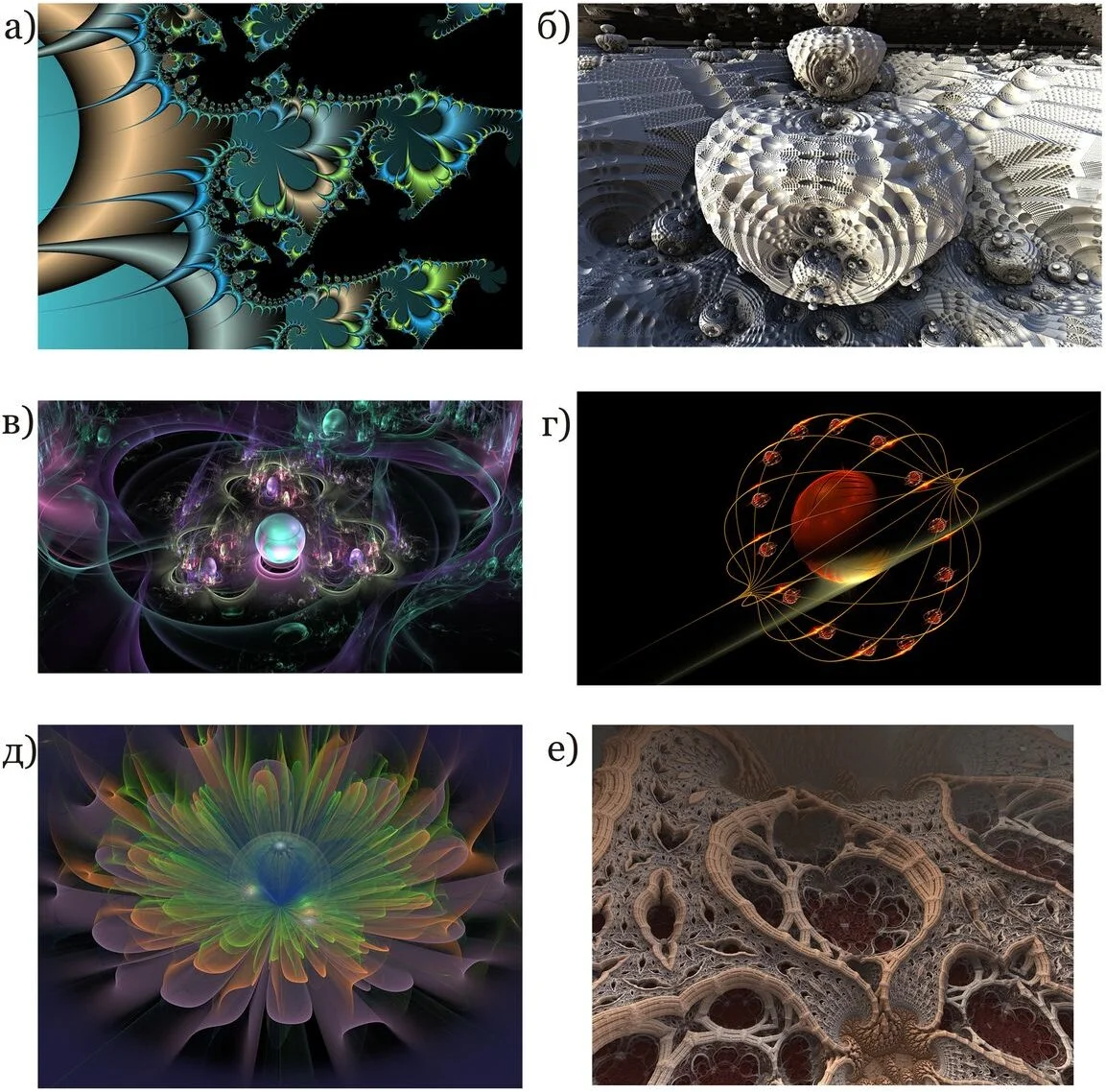
Обычно IFS используется для построения листьев, цветов, веток, деревьев и кустарников при создании реалистичных картин в компьютерном дизайне и играх. На рис. 9 приведены примеры изображений, полученных на основе IFS: лист папоротника (а), коралл (б), дракон (в), спираль (г), дерево (д, е); изображения получены в программе Graphic x4.2007.
Для качественного отображения на основе IFS требуется достаточно большое количество итераций. Так, для изображений, представленных на рис. 9, использовано от 100 тыс. до 300 тыс. итераций.

Алгебраические фракталы
Эта группа фракталов строится на основе алгебраических формул, зачастую очень простых [2, 6, 8, 22]. Различают линейные и нелинейные алгебраические фракталы. Первые определяются линейными функциями (уравнениями первого порядка), а вторые — нелинейными (их природа значительно ярче, богаче и разнообразнее).
В общем виде фракталы данного класса могут быть получены на основе рассмотрения некоторых нелинейных процессов в n-мерных пространствах (в настоящее время наиболее изучены лишь двухмерные процессы). В связи с этим любой рассматриваемый нелинейный итерационный процесс может интерпретироваться как дискретная динамическая система.
Как известно (из синергетических представлений), нелинейные динамические системы могут иметь несколько устойчивых состояний. При этом состояние, в котором оказалась динамическая система после определенного конечного числа итераций, напрямую зависит от ее начального состояния. А это значит, что изучаемая система может рассматриваться в некотором фазовом пространстве, в котором будут присутствовать области притяжения (аттракторы). Рассматривая двумерное фазовое пространство и окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет любой системы. Применение различных алгоритмов выбора цвета позволяет получить достаточно сложные фрактальные картины с удивительными многоцветными узорами.
Классическим примером алгебраических фракталов является множество Мандельброта, описанное еще в 1905 г. французским математиком Пьером Фату и впервые построенное Мандельбротом в 1980 г. Алгоритм построения множества Мандельброта использует единственную простую итерационную формулу:
,
где z и c — комплексные величины, i — номер итерации.
В результате многократных итераций на плоскости образуется множество точек, выстраивающихся в сложной закономерности (рис. 10).
Доказано, что все точки, составляющие множество Мандельброта, целиком расположены внутри круга радиуса 2 на плоскости с центром в точке (0, 0). На практике при построении множества Мандельброта принято считать, что если для некоторой точки А последовательность итераций функции после некоторого их числа N (например, превышающих 100) не вышла за пределы этого круга, то точка принадлежит множеству и красится в черный цвет. Если же на какой-то итерации, меньшей N, элемент последовательности, определяемый на основе (1) по модулю стал больше 2, то он считается не относящимся к множеству. Основываясь на таком правиле, можно получить черно-белое изображение множества Мандельброта.

Однако черно-белое множество не так привлекательно, поэтому в настоящее время принято отображать множества в цвете. Для этого можно, например, каждую точку не из множества красить в цвет, соответствующий номеру итерации, на котором ее последовательность выходит за пределы круга. Так, на рис. 10 при отображении множества Мандельброта применен наиболее распространенный способ построения цветного изображения множества, при котором точки, принадлежащие множеству, окрашиваются в черный цвет, а не принадлежащие множеству окрашиваются в цвет, соответствующий количеству итераций, за которое точка покидает окружность (построение выполнено в программе Fractal Explorer 2.02). Точки на границе множества, где возникают сложные структуры, уходят в бесконечность за конечное число итераций (аттрактор такой динамической системы находится в бесконечности).
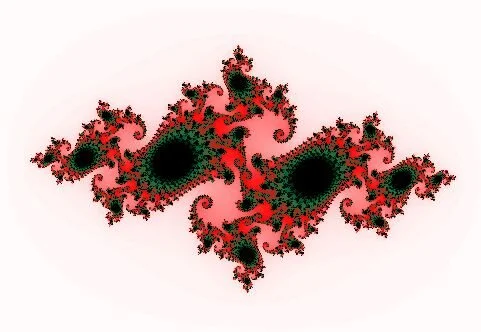
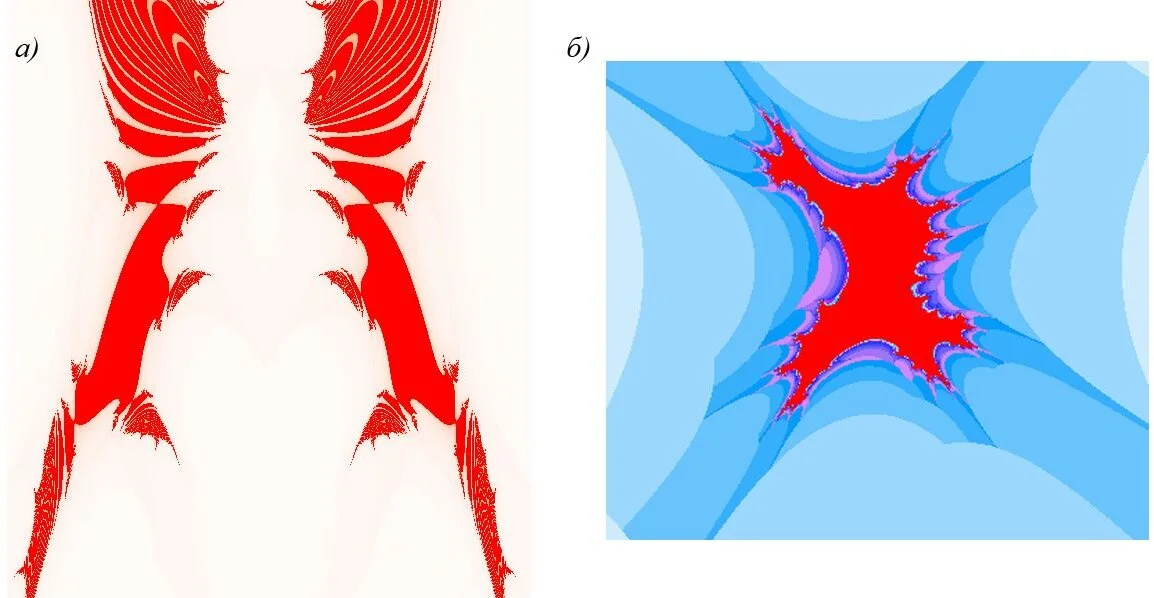
К наиболее известным алгебраическим фракталам также относятся множества Жюлиа (рис. 11 — построение выполнено в программе Graphic v4.2007, рис. 12 — построение выполнено в программе Фракталы) и Бассейны Ньютона (рис. 13, построение выполнено в программе Fractal Explorer 2.02, рис. 14 — построение выполнено в программе Ultra Fractal 5).
Семейство множеств Жюлиа строится по той же итерационной формуле, что и множество Мандельброта, однако в качестве комплексной переменной используется лишь параметр c. Если в качестве значений комплексной переменной c использовать координаты точек, принадлежащих множеству Мандельброта, то множество Жюлиа при построении будет замкнутым.



Стохастические фракталы
При построении таких фракталов случайным образом изменяют некоторые параметры, определяющие структуру фрактала. При этом можно получить объекты, очень похожие на природные, которые демонстрируют несимметричные деревья, изрезанность береговых линий, модели рельефов местности и поверхности морей.
Двумерные стохастические фракталы очень часто используются для моделирования рельефа местности и поверхности моря [2].
Некоторые примеры стохастических фракталов приведены на рис. 15 и 16 (изображение на рис. 16 сгенерировано программой Apophysis 7x).

Другие примеры фрактальных изображений
Рассмотрим еще некоторые примеры фрактальных структур. На рис. 17 и 18 приведены примеры реальных природных форм, демонстрирующих фрактальную структуру.
На рис. 17 показана фотография раковины моллюска. Видно, что каждая отдельная «комнатка» является уменьшенной версией предыдущей.
На рис. 18 показано фото цветной капусты Романеско, форма которой похожа на фрактал (это позволяет назвать ее естественным фракталом). Однако самоподобная структура капусты повторяется лишь несколько раз, и прекращается на более мелких уровнях.
На рис. 19 показан пример изображения, полученного в программе Fractal Explorer 2.02.
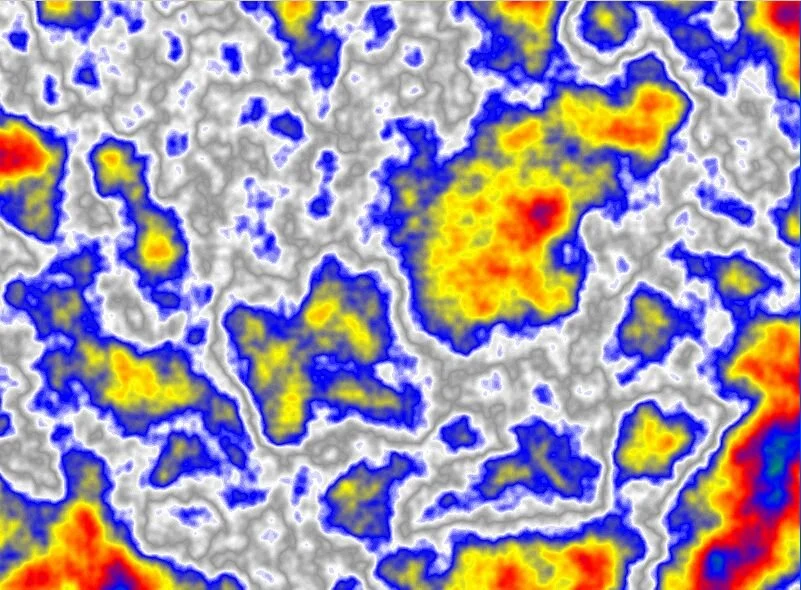
На рис. 20 и 21 показаны примеры фрактальных изображений, полученных в программе ChaosPro 4.0. Стоит отметить, что фрактал «Плазма» сильно напоминает срез пористой среды, особенно если перевести изображение в оттенки серого.



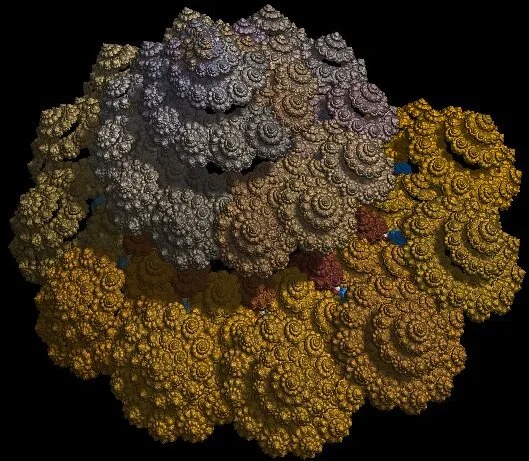
Огромное количество разнообразных изображений фракталов можно найти на сайте https://pixabay.com/ и использовать их по своему усмотрению (бесплатно). Ниже на рис. 22 (а) — (е) приведены некоторые из них.