В настоящее время большое количество научной литературы посвящено исследованиям разнообразных финансовых инструментов методами нелинейной динамики и теории хаоса. Вероятностное описание котировок финансовых инструментов, впервые введенное Башелье, основывалось на их независимости и гауссовом распределении изменений цен. Простая и удобная в использовании модель, предложенная Башелье, однако, плохо описывала происходящее на рынке. Модель, в частности, оказалась неспособной учитывать долговременные корреляции и «толстые хвосты» в распределениях доходностей финансовых инструментов, которые они демонстрируют.
В 1963 году в динамической системе, при изучении турбулентности, Лоренцем [26] было обнаружено очень сложное движение, которое воспринималось как хаотическое. Для характеристики таких движений впервые ввели понятие динамического хаоса. В статье Рюэля и Такенса [27], опубликованной в 1971 году, был введен новый математический образ динамического хаоса — странный аттрактор. Определение «странный» подчеркивает два основных свойства аттрактора. Во-первых, необычность его геометрической структуры. Размерность странного аттрактора является дробной (фрактальной). Во-вторых, странный аттрактор — это притягивающая область для траекторий из окрестных областей. При этом все траектории внутри странного аттрактора динамически неустойчивы, что выражается в сильной экспоненциальной расходимости близких в начальный момент траекторий.
Схожесть в поведении хаотических систем и экономических рынков привела к идее, что за движение котировок на рынке акций может определяться вполне определенной динамической системой [11]. Объяснение наблюдаемой фрактальной структуры финансовых данных было предложено Мандельбротом с помощью мультифрактальной модели доходностей акций. Особенное внимание уделялось также проблеме корректности применения нелинейного прогнозирования в области финансовых временных рядов (LeBaron B., Chaos and Nonlinear Forecastability in Economics and Finance, Philosophical Transactions of the Royal Society of London 348, 1994;).
Тем не менее, большинство представленных работ представляют собой изящные теоретические выводы и почти не содержат практических рекомендаций по их применению в прикладных задачах. Настоящая работа посвящена решению прикладных задач нелинейного анализа реальных котировок акций. Особенное внимание уделяется проверке корректности полученных с помощью существующих на сегодняшний день программных продуктов результатов.
Обзор используемого программного обеспечения
Для динамического анализа данных использовались следующие программные продукты: программа Dataplore компании DATAN, набор модульных программ TISEAN, созданных в Институте физики и теоретической химии университета города Франкфурта Райнером Хеггером (Rainer Hegger), Ольгером Канцом (Holger Kantz) и Томасом Шрайбером (Thomas Schreiber), Chaos Data Analyzer (CDA), написанная Дж. Спроттом и Дж. Роуландсом (Sprott J., Rowlands G.), а также программа Fraclan, разработанная в институте математических проблем биологии РАН В. Сычевым.
Для фрактального анализа в работе использовался специализированный набор расширений (toolbox) программы MatLab — FracLab, созданный во французской лаборатории Fractals team.
Линейная парадигма
Кратко напомним основные предположения гипотезы эффективного рынка [10]. Гипотеза эффективного рынкапредполагает, что цены отражают всю публичную информацию. Изменения в ценах никак не соотносятся между собой, разве что для очень коротких временных зависимостей, которые быстро исчезают. Рыночная стоимость определяется консенсусом большого количества аналитиков.
Рациональные инвесторы оценивают прибыль методом вероятностного взвешивания, который дает ожидаемые прибыли. Риск измеряется как стандартное отклонение прибылей. Инвесторы предпочитают активы, которую дают наивысшую ожидаемую прибыль при заданном уровне риска. Инвесторы не склонны к риску. Вследствие двух названных выше концепций цены следуют случайному блужданию. Следовательно, вероятностное распределение приблизительно нормально или логнормально. Эта приблизительность означает, как минимум, что распределение прибылей имеет конечную среднюю величину и дисперсию.
Эти предположения указывают на то, что теория рынков капитала существенно зависит от нормальности распределения прибылей. Но, как уже упоминалось выше, эмпирические исследования зачастую опровергают данное предположение. Большинство инвесторов не реагируют на поступившую информацию сразу же после ее получения, а ждут ее подтверждения, ничего не предпринимая до тех пор, пока тренд не станет явно установившимся. Такое движение соответствует обобщенному броуновскому движению, описываемому фрактальной геометрией. [10] Результаты исследований статистического анализа, показывают, что основные свойства финансовых инструментов на рынке не совпадают с предсказанными гипотезой эффективного рынка результатами.
Фазовое пространство, восстановление фазового пространства
Главная идея применения методов хаотической динамики к анализу временных рядов состоит в следующем. Оказывается [15], основная структура хаотической системы, содержащая в себе всю информацию о системе, а именно, ее аттрактор (подмножество фазового пространства, притягивающее траектории в пределе бесконечного времени), может быть восстановлена через измерение только одной наблюдаемой этой динамической системы, фиксированной как временной ряд.
Детерминированные динамические системы описывают эволюцию системы с течением времени в некотором фазовом пространстве
Эти системы могут быть порождены, например, обыкновенными дифференциальными уравнениями
или, если время дискретно t = nΔt, выражениями вида
Временные ряды затем можно рассматривать как последовательность наблюдений { Sn = S(xn) }, сделанных с помощью некоторой функции измерения s(.) . Так как последовательность (обычно скалярная) { Sn } сама по себе не порождает многомерное фазовое пространство динамической системы, необходимо использовать некоторый технический прием, чтобы раскрыть многомерную структуру, используя только имеющиеся данные.
Согласно методу Грасбергера и Прокаччи [14], процедура реконструкции фазового пространства и восстановления хаотического аттрактора системы при динамическом анализе временного ряда, сводится к построению так называемого лагового или восстановленного пространства с помощью метода задержки(method of delays). Векторы в новом пространстве, пространстве вложения, сформированы из значений временного ряда скалярных измерений с временным запаздыванием:
Число элементов m называется размерностью вложения, время τ обычно называется задержкой или лагом. В теоремах Такенса [16] и Сойера [17] показывается, что если последовательность { Sn } на самом деле состоит из скалярных измерений структуры динамической системы, тогда, при определенных предположениях, такое восстановление фазового портрета является точной картиной настоящего множества { x }, если, конечно, m достаточно велико.
Или, другими словами, реальный аттрактор динамической системы и «аттрактор», восстановленный в лаговом пространстве по временному ряду согласно указанному выше правилу (псевдоаттрактор), при адекватном подборе размерности вложения m, являются топологически эквивалентными и обладают одинаковыми обобщенными фрактальными размерностями, ляпуновскими показателями и другими численными характеристиками.
В том случае, если анализируемый временной ряд является реализацией случайного процесса, то восстановленный псевдоаттрактор представляет собой бесструктурное облако точек, которое при последовательном бесконечном увеличении размерности вложения лагового пространства m, подобно газу, заполняет весь предоставленный ему объем [15].
Метод задержки для восстановления фазового портрета широко используется в динамическом анализе временных рядов. Практическая реализация этого метода проста и не требует детального объяснения. Напомним лишь, что если временной ряд содержит N измерений, то число вложенных векторов равно N — (m — 1) τ. Это необходимо помнить для правильной нормировки усредненных значений.
Требования к анализируемым данным
Для вычисления характеристик псевдоаттрактора, таких как его фрактальная размерность, показатели Ляпунова, необходимо иметь множество точек, определенных в фазовом пространстве размерности m и принадлежащих аттрактору. Число точек M в расчетах конечно, но обязано быть достаточно большим. Согласно формуле, предложенной в [18]
где D — размерность аттрактора. Исходя из этого выражения, нами было выбрано такое количество данных, которое вполне соответствовало бы малоразмерной динамике движения, с размерностью n ≤ 4. В соответствии с этими рассуждениями было принято решение остановиться на длине временных рядов равной 3363 измерениям. Эти измерения представляют собой динамику движения котировок акций за период с января 1990 года по май 2003 года.
Параметры вложения
Разумный выбор временного лага является важной задачей, так как всегда приходится иметь дело с зашумленными временными рядами конечной длины. В зависимости от типа исследуемой структуры приходится выбирать подходящий временной лаг. Например, единичная задержка для дискретных данных даст вектора, сконцентрированные вокруг диагонали в пространстве вложения и, таким образом, вся структура, перпендикулярная к диагонали, будет практически невидима. [13]
Для описания данной проблемы в работе [19] были введены понятия избыточности (redundancy) и неуместности (irrelevance). Небольшие временные задержки порождают сильно коррелированные векторы, большие, в свою очередь, приводят к векторам, чьи компоненты практически не коррелируют между собой, и данные, таким образом, будут произвольно распределены в пространстве вложения.
Утверждается [20-22], что оптимальная размерность вложения может быть определена (если это вообще возможно) только для определенной задачи, для которой мы и рассматриваем вложение. Тем не менее, некоторые численные инструменты, подсказывающие нам, как сделать выбор, все же существуют. Наиболее известными из таких инструментов являются метод ложных ближайших соседей (False Nearest Neighbors) и метод взаимной информации (Mutual Information). Еще раз отметим, что выяснение разумной размерности вложения вне конкретной задачи не является возможным.
Определение оптимальной временной задержки τ
Для малых интервалов времени Δt значения измерений Sk и Sk+1 будут близкими, поэтому задача правильного выбора временной задержки τ является одной из наиболее важных. Необходимо выбрать τ так, чтобы корреляция между sk и sk+1 стремилась к нулю. Традиционный способ выбора временной задержки состоит в вычислении автокорреляционной функции временного ряда:
Задержка τ выбирается равной времени первого пересечения нуля автокорреляционной функции. Этот метод достаточно прост, но необходимо помнить, что автокорреляционная функция не учитывает нелинейные корреляции в данных.
Другой способ [23] требует вычисления спектра мощности временного ряда, т.е. быстрого преобразования Фурье автокорреляционной функции. Если в спектре мощности присутствуют кратные пики, то задержка τ выбирается равной четверти периода самой высокой из доминирующих частот.
Третий способ [24] основан на вычислении функции задержанной взаимной информации (time delayed mutual information). Функция взаимной информации S определяется следующим образом:
где для некоторого разбиения вещественных данных pi — вероятность найти значение временного ряда в i-оминтервале разбиения, а Pij(τ) — совместная вероятность того, что наблюдаемая величина попадет в i-ый интервал, а время этого наблюдения далее попадет в j-ый интервал. Теоретически, это выражение не зависит от размера разбиения и, таким образом, может быть просто сосчитано. Предполагается [24], что если задержанная взаимная информация имеет минимум в некоторый момент времени τ, то это значение времени может рассматриваться в качестве оптимального значения временной задержки τ.
Определение оптимальной размерности вложения
Метод определения минимальной достаточной размерности вложения m был предложен M. Кеннелом [25]. Он получил название метод ложного ближайшего соседа. Идея метода достаточно проста. Предположим, что минимальная размерность вложения данного временного ряда { Si } равна m0. Это означает, что восстановленный в m0-мерном пространстве псевдоаттрактор является взаимно-однозначным образом аттрактора в оригинальном фазовом пространстве. Особо отметим тот факт, что у восстановленного аттрактора сохранены топологические свойства оригинала.
Таким образом, соседи некоторой выбранной точки отображены на соседей в восстановленном фазовом пространстве. Учитывая предположение о гладкости динамического процесса, окрестности точек также должны отобразиться в окрестности точек на псевдоаттракторе. Кроме того, форма и диаметр окрестностей изменяются в соответствии с показателями Ляпунова.
Но, предположим, что ряд погружается в m-мерное пространство с m 0. Вследствие такой процедуры топологическая структура аттрактора изменилась. Некоторые точки спроецировались в окрестности других точек, хотя не будут принадлежать им в пространстве более высокой размерности. Эти точки называются ложными соседями. Если дополнительно наложить некоторую динамику, то эти ложные соседи обычно отображаются не в образ окрестности, а куда-нибудь еще, так, что средний «диаметр» окрестности становится совсем большим.
Идея программной реализации метода следующая. Сначала восстанавливается фазовое пространство с помощью метода Грасбергера и Прокаччи. Векторы в этом пространстве определяются согласно формуле (3). Для каждой точки Si временного ряда, ищется его ближайший сосед Sj в m-мерном пространстве. Вычисляется расстояние между ними
Далее, итерируем обе точки и вычисляем
Если Ri превышает данный эвристический порог Rt, то считается, что точка имеет ложного ближайшего соседа [25]. Критерием того, что размерность вложения достаточна, является равенство нулю или, по крайней мере, достаточная близость к нему доли точек, для которых (Ri>Rt) .
Введение концепции ложного ближайшего соседа и других специальных инструментов стало своего рода реакцией на тот факт, что большая часть результатов оценки нелинейных характеристик, подобных корреляционной размерности, была ошибочной в связи с некорректной процедурой оценки. Например, слабые корреляции и случайные колебания часто ошибочно принимались за нелинейную динамику. Реализация FNN, однако, позволяет избежать ошибочного оценивания размерности посредством правильного определения минимального временного разделения «правильных» соседей.
Анализ литературы, посвященной FNN-анализу, показал, что в настоящее время не существует определенного критерия, который смог бы объяснить, какое именно значение отношения числа ложных соседей ко всем соседям является «достаточно малым», чтобы можно было принять гипотезу о достаточном значении размерности вложения. Часто в реальных данных наблюдается малые осцилляции около нулевого значения этого отношения, при этом число ложных соседей очень мало. Напрашивается предположение, согласно которому гипотезу о достаточности величины размерности вложения можно принимать при определенном уровне ее значимости. Данный подход к разрешению возникшей проблемы при анализе реальных временных рядов кажется достаточно релевантным, но требует более детального анализа с точки зрения математической статистики, который выходит за рамки данной работы. Тем не менее, далее в работе будет сделана попытка ввести определенный уровень значимости гипотезы, исходя только из эмпирических наблюдений.
Также следует заметить, что, по-видимому, значение размерности вложения, при которой число ложных соседей становится равным нулю, а, следовательно, и отношение числа ложных соседей ко всем становится равным нулю, определяет верхнюю границу значения искомой размерности псевдоаттрактора, что также далее будет обсуждаться на примере реальных данных.
Корреляционная размерность, корреляционная сумма
Один из тестов, применяемых на практике для проверки наличия хаотической составляющей в изучаемом ряде финансовых данных, состоит в изучении свойств корреляционной суммы Cm(r) и поведения корреляционной размерности Dm(r) в зависимости от размерности вложения m. Корреляционная сумма Cm(r) — это вероятность того, что пара точек на восстановленном аттракторе в m-мерном лаговом пространстве находится в пределах расстояния r друг друга. Если график функции ln Cm(r) относительно ln r имеет отчетливо выраженный линейный участок, это указывает на существование самоподобной геометрии аттрактора [10,21], что, в свою очередь, говорит о хаотичности финансового инструмента. Написано достаточно много статей, посвященных корректной оценке корреляционной размерности и типичным ошибкам при ее вычислении. Среди этих работ можно выделить [20,21,31,32].
В случае стилизованных данных, когда нам известна размерность n фазового пространства динамической системы и все n координат каждой точки на аттракторе, корреляционную размерность D2 аттрактора находят следующим образом [14, 29]: рассматривается корреляционный интеграл C(r), показывающий относительное число пар точек аттрактора, находящихся на расстоянии, не большем r:
где θ — функция Хевисайда, ρ — расстояние в n-мерном фазовом пространстве, m — число точек xi на аттракторе. На достаточно малых масштабах длин и когда размерность вложения m не меньше топологической размерности аттрактора, выполняется зависимость [30]:
где D2 — искомая корреляционная размерность аттрактора. Прологарифмируем уравнение (9):
Выражение (10) дает искомую оценку размерности аттрактора как тангенс угла наклона прямой, аппроксимирующей график корреляционного интеграла C(r) в двойном логарифмическом масштабе.
Справедливость степенного закона (9) ограничена значениями r, малыми по сравнению с размером аттрактора. При очень малых значениях r число пар точек (xi,xj), расстояние между которыми не превышает r, становится малым из-за конечности числа точек на аттракторе, и статистика становится бедной. При r, сравнимых с размером аттрактора величина C(r) быстро достигает насыщения C(r) → 1. В случае реальных данных степенной закон выполняется только в ограниченном диапазоне значений r, который и может быть использован для определения размерности аттрактора.
При увеличении размерности вложения корреляционная размерность увеличивается. Однако для хаотических данных корреляционная размерность будет, в конечном счете, насыщаться при ее истинном значении. Для случайных данных такого насыщения не наблюдается, и корреляционная размерность растет монотонно. Чтобы объяснить такое поведение корреляционной размерности, заметим, что в рамках метода Грасбергера и Прокаччи [14], корреляционная размерность для реальных хаотических систем является хорошим приближением для фрактальной размерности странного аттрактора. Фрактал, вложенный в пространство с более высокой размерностью, сохраняет свою истинную размерность из-за нелинейных корреляций между точками. Поэтому для детерминированного хаотического временного ряда корреляционная размерность сходится к ее истинному значению. В то же самое время для случайной последовательности, как уже отмечалось выше, точки восстановленного псевдоаттрактора образуют бесструктурное облако в лаговом пространстве вне зависимости от его размерности [15].
Отметим, что в случае экспериментальных данных мы не знаем априори размерность фазового пространства динамической системы, имея на руках только временной ряд, порожденный ею. Для получения правильной оценки необходимо проверить корреляционную размерность на сходимость при возрастающем значении размерности вложения. Как правило, хаотические детерминированные системы маломерны. Эффект добавления шума приводит к увеличению корреляционной размерности. Обратим внимание, что корреляционная размерность большая, чем пять, подразумевает, по существу, случайные данные [15].
Реальные финансовые временные ряды обычно зашумлены, поэтому важным вопросом в исследовании временных рядов является анализ влияния шума на получаемые результаты. В частности, в работе Х. Канца и Т. Шрайбера [33] приведен анализ влияния аддитивного белого шума на получаемое значение корреляционной размерности. Рассмотрим сигнал, который может быть точно восстановлен в n-мерном фазовом пространстве. Если мы восстановим такой сигнал в (n+1)-мерном пространстве, то корреляционная размерность D2(ε,n+1) будет связана с размерностью D2(ε,n) по формуле [33]:
где n — размерность вложения, ε = r / rmax — нормированное расстояние, rmax — максимальное расстояние между двумя точками на восстановленном аттракторе, σ — уровень шума, равный стандартному отклонению, а
— интеграл ошибок.
Важное следствие этого аналитического результата состоит в том, что даже при ε = 3σ корреляционная размерность заметно увеличивается с ростом размерности вложения, а именно, на 0.2 при переходе от n к n+1 [33].
R/S — анализ и показатель Херста
Вычисление показателя Херста производится с помощью метода нормированного размаха (Rescaled Range (R/S) Analysis). Основной целью вычисления показателя Херста является определение долговременной корреляции во временном ряде, и выявление его фрактальной структуры. Кроме того, отметим, что с помощью R/S-анализа можно обнаружить существующие в динамике системы статистические циклы [10]. Методика проведения R/S анализа описана ниже. Пусть Yt — цена акции в момент времени t. Тогда временной ряд логарифмических доходностей строится следующим образом:
Построим также кумулятивную сумму:
Затем найдем размах (range)R(Δt):
Посчитаем стандартное отклонение S(Δt) величины ξt на временном интервале длины Δt
Нормируем размах R(Δt) на среднеквадратичное отклонение S(Δt), и усредним это значение по n интервалам разбиения:
Если оказалось, что
, где H — константа, то такие временные ряды называется процессами Хёрста [52].
Для того, чтобы установить связь показателя Херста с коэффициентом корреляции, необходимо принять гипотезу о том, что финансовые временные ряды представляют собой обобщенное броуновское движение.
Обобщенное броуновское движение
Среди множества случайных процессов выделим узкий класс, который характеризуется определенными свойствами. Пусть { BH (t) }t>0 — случайный процесс, который нормально распределен с параметром (0, 1, H), а именно [52]:
где
, а
Δt>0
Такой случайный процесс называется обобщенным броуновским движением. Из выражения (15), в частности, следуют следующие свойства обобщенного броуновского движения:
- Математическое ожидание приращений броуновского движения равно 0, а именно.
- Дисперсия приращений броуновского движения зависит от времени таким образом.
Отметим, что классическое броуновское движение получается из обобщенного броуновского движения как частный случай при H=0.5. Рассмотрим приращения обобщенного броуновского движения (ОБД) вперед и назад и используем свойство 1:
Посчитаем коэффициент корреляции приращений ОБД:
Учитывая, что
(свойство 1), приходим к следующему выражению:
Прежде всего, заметим, что при H=0.5 корреляция прошлых и будущих приращений равна 0 при всех t, как и должно быть для случайного процесса с независимыми приращениями. Однако при H≠0.5 получается C(t)≠0 независимо от t. Это свойство обобщенного броуновского движения заключается в персистентности (сохранении тенденции) и антиперсистентности [52]. Отметим, также, что в современной теории ценообразования показатель Херста рассматривается иногда как мера волатильности котировок.
В соответствии со значением показателя Херста, все временные ряды могут быть классифицированы на три типа [10]:
- антиперсистентные временные ряды (0
- случайные временные ряды (H=0.5);
- персистентные временные ряды (0.5
Под случайными временными рядами здесь будем понимать такие ряды, которые имеют независимые приращения. Функция плотности вероятности распределения может быть нормальной (гауссовской), однако это не обязательное условие. R/S — анализ может классифицировать произвольный ряд, безотносительно к тому, какой вид функции распределения ему соответствует.
Антиперсистентные временные ряды соответствуют типу систем, часто называемых «возврат к среднему» — если система демонстрирует рост в предыдущем интервале времени, то вероятнее всего, что в следующем периоде начнется спад. И наоборот, если шло снижение, то вероятен близкий подъем. Устойчивость такого антиперсиситентного поведения зависит от того, насколько близко значение H к нулю. Антиперсистентный ряд более изменчив, чем ряд случайный, так как состоит из частых смен фаз подъема и спада.
Персистентные или трендустойчивые ряды характеризуются следующим типом поведения: если ряд возрастает (убывает) в предыдущий период, то, вероятно, что он будет сохранять эту тенденцию какое-то время в будущем, то есть система в среднем сохраняет свой тренд. Сила персистентности увеличивается при приближении показателя Херста к единице, т.е. стопроцентной корреляции.
Перемешивание данных и разрушение корреляций
Обоснованность оценки показателя Херста можно проверить путем случайного перемешивания данных, в результате чего порядок наблюдений станет полностью отличен от исходного ряда. Ввиду того, что наблюдения остаются теми же, их частотное распределение остается неизменным. Далее вычислим показатель Херста этих перемешанных данных. Если ряд действительно являлся независимым, то показатель Херста не изменится, поскольку отсутствовал эффект долговременной памяти, то есть корреляции между наблюдениями. В этом случае перемешивание данных не оказывает влияние на качественные характеристики данных.
Если имел место эффект долговременной памяти, то порядок данных весьма важен. Перемешивая данные, мы тем самым разрушаем структуру системы. Оценка показателя Херста при этом должен измениться и приблизиться к 0.5, даже если частотное распределение наблюдений не изменилось.
Результаты исследования и их анализ
Результаты разделены на разделы. Каждое из вычислений будет проверено на стилизованных данных, для которых известен теоретический результат. В заключение каждого исследования будет сделан вывод о правильности реализации описанных выше алгоритмов в программных продуктах.
Показатель Херста
Задача нахождения показателя Херста является очень важной с точки зрения получения информации о характере движения котировок акций, в частности, в работе [10] предлагается использовать показатель Херста в качестве меры риска той или иной акции или иной ценной бумаги. Проблема на сегодняшний день заключается в том, что большинство существующих программных продуктов дают сильно смещенную оценку показателя Херста. Исследования значений показателя Херста проводились в трех различных программных продуктах — CDA, Fraclan, Dataplore. На вход CDA и Dataplore необходимо подавать исходный ряд. Для подсчета показателя Херста в программе Fraclan на вход необходимо подавать логарифмические доходности. Отметим также, что CDA и Fraclan определяют показатель Херста из наклона линейной аппроксимации кривой R/S в двойном логарифмическом масштабе, тогда как в Dataplore используется степенная аппроксимация отношения R/S. В качестве стилизованных данных были взяты оригинальные и перемешанные фрактальные броуновские движения с показателями Херста H=0.3 H=0.5 и H=0.8. Результаты исследования модельных данных приведены в таблице 1.
| Моделирующие значения H | Fraclan | CDA | Dataplore | ||||
| H | ΔH | H | ΔH | H | ΔH | ||
| 0.3 | неперемешанные | 0.27 | 0.08 | 0.35 | - | 0.42 | - |
| перемешанные | 0.58 | 0.11 | -0.0007 | - | 0.13 | - | |
| 0.5 | неперемешанные | 0.51 | 0.10 | 0.49 | - | 0.41 | - |
| перемешанные | 0.51 | 0.11 | 0.0008 | - | 0.09 | - | |
| 0.8 | неперемешанные | 0.76 | 0.21 | 0.77 | - | 0.74 | - |
| перемешанные | 0.40 | 0.13 | 0.0017 | - | 0.05 | - | |
Анализ стилизованных данных показывает, что наилучшую оценку показателя Херста дает программа Fraclan. Среди ее достоинств следует также отметить быстроту выполнения оценки и вычисление ее погрешности. Использование CDA и Dataplore для оценки показателя Херста показало, что обе программы более или менее точно определяют значение искомой величины, но для перемешанных данных выдают совершенно необъяснимые результаты, что позволяет предположить некорректность используемых в них алгоритмов. Ниже, в таблице 2, приведены оценки показателя Херста для исследуемых в работе временных рядов. В качестве таковых были взяты котировки акций 30-ти компаний, входящих в индекс Доу-Джонс.
| Компания | H | ΔH | Компания | H | ΔH |
| AA | 0.37 | 0.13 | IP | 0.33 | 0.13 |
| AXP | 0.50 | 0.11 | JNJ | 0.46 | 0.13 |
| BA | 0.44 | 0.16 | JPM | 0.47 | 0.11 |
| С | 0.42 | 0.18 | KO | 0.54 | 0.15 |
| CAT | 0.43 | 0.10 | MCD | 0.49 | 0.19 |
| DD | 0.51 | 0.17 | MMM | 0.39 | 0.13 |
| DIS | 0.41 | 0.18 | MO | 0.48 | 0.11 |
| EK | 0.54 | 0.21 | MRK | 0.53 | 0.15 |
| GE | 0.49 | 0.15 | MSFT | 0.50 | 0.11 |
| GM | 0.44 | 0.14 | PG | 0.42 | 0.12 |
| HD | 0.50 | 0.14 | SBC | 0.48 | 0.16 |
| HON | 0.47 | 0.15 | T | 0.53 | 0.13 |
| HPQ | 0.48 | 0.21 | UTX | 0.49 | 0.15 |
| IBM | 0.64 | 0.10 | WMT | 0.51 | 0.14 |
| INTC | 0.47 | 0.19 | XOM | 0.56 | 0.12 |
Отметим, что оценка показателя Херста для большинства котировок лежит в окрестности H=0.5. Если полученные результаты релевантны, это позволяет предположить, что сложившаяся на данный момент ситуация на рынке ценных бумаг США достаточно неблагоприятна для краткосрочного прогнозирования. Исключениями являются акции компаний IBM и IP, значения показателя Херста которых даже в пределах погрешности отличаются от H=0.5. Ряд IBM, если быть точным, демонстрирует персистентный характер движения, а IP, наоборот, антиперсистентный. Отметим также, что показатель Херста может быть удобным показателем меры рискованности активов — чем ближе показатель Херста к значению 0.5, тем с меньшей уверенностью можно утверждать что-либо о характере будущего движения.
Вычисление корреляционной размерности
Выше было отмечено, что определение корреляционной размерности временного ряда финансовых данных является одним из основных тестов, применяемых на практике для выяснения наличия в них хаотической составляющей. Оценка корреляционной размерности должна проводится для детрендированных логарифмов данных. [15] Среди всех программных продуктов, используемых в ходе исследований, процедуру оценки корреляционной размерности выполняют лишь две программы: CDA и Fraclan. Протестируем их на стилизованных данных отображения Хенона и системы Лоренца.
Значения временной задержки в программе Fraclan выбираются согласно критерию локального минимума взаимной информации, в то время как CDA не предоставляет возможности анализировать функцию взаимной информации и выбирать оптимальное значение τ (выбор ограничен значениями τ, которые являются степенью 2).Кроме того, время, затраченное на оценку корреляционной размерности с помощью программы CDA на порядок больше, чем с помощью Fraclan. Ниже, на рисунках Г-Ж, приведены графики зависимости корреляционной размерности от размерности вложения. Оценка корреляционной размерности описанных выше стилизованных данных обеими программами приведена в таблице 3.
Занесем результаты оценки в таблицу и проанализируем их. На стилизованных данных обе программы дают весьма точную оценку корреляционной размерности. Но следует отметить, что для приведенных стилизованных примеров оптимальное значение задержки для восстановления фазового портрета равно 1.
| Название системы | Fraclan | CDA | ||||
| D2 | ΔD2 | m | D2 | ΔD2 | m | |
| Хенон | 1.197 | - | 2 | 1.312 | 0.197 | - |
| Лоренц | 2.067 | - | 4 | 2.070 | 0.020 | - |
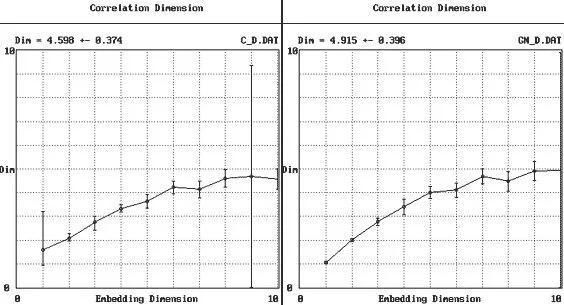
В случае реальных данных подобное значение оптимальной задержки встречается очень редко, следовательно, необходимо с осторожностью подходить к результатам, полученным с помощью CDA. Забегая вперед, скажем, что оценка корреляционной размерности с помощью CDA довольно часто давала необъяснимые результаты. Особенно яркими примерами несостоятельности алгоритма определения корреляционной размерности, используемого в CDA, служат результаты, полученные для временных рядов С и GM (рис. 1). В обоих случаях ошибка оценки размерности при определенной размерности вложения без видимых причин вырастает до значения корреляционной размерности. Кроме этого, в первом случае результат оценки корреляционной размерности при размерности вложения, равной 1, вообще лишен физического смысла, так как корреляционная размерность не может быть больше топологической размерности пространства вложения [45].
Перед тем, как перейти к анализу временных рядов котировок исследуемых акций, поясним некоторые детали алгоритма определения релевантной корреляционной размерности, реализованного в программе Fraclan. Программа последовательно увеличивает размерность вложения и запоминает полученные значения корреляционной размерности. Как только вычисленная оценка корреляционной размерности насыщается и не превосходит максимального значения при увеличении размерности вложения в течение двух итераций, все расчеты останавливаются. Максимальное значение оценки корреляционной размерности при этом считается наиболее правильной оценкой корреляционной размерности, а размерность вложения, при которой было достигнуто это максимальное значение, считается оптимальной размерностью вложения. Это достаточно сильное утверждение, конечно, нуждается в доказательстве, но, тем не менее, мы примем его без дополнительного обсуждения.
На рис. 2 приведен один из графиков зависимости корреляционной размерности от размерности вложения для временных рядов котировок исследуемых акций. По оси абсцисс отложена размерность вложения, а по оси ординат — значение корреляционной размерности.
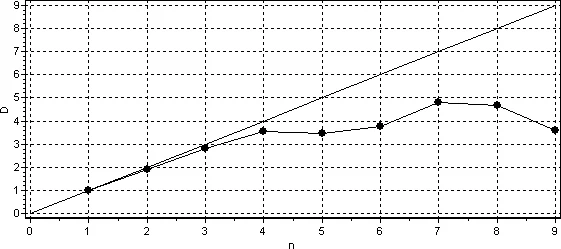
После объединения результатов исследования в таблицу 4, проанализируем ее.
| Компания | D2 | m | Компания | D2 | m |
| AA | 3.799 | 4 | IP | 5.377 | 6 |
| AXP | 4.788 | 7 | JNJ | 4.641 | 6 |
| BA | 4.165 | 5 | JPM | 3.951 | 4 |
| С | 4.234 | 8 | KO | 2.977 | 3 |
| CAT | 3.389 | 8 | MCD | 4.895 | 7 |
| DD | 5.136 | 7 | MMM | 5.919 | 10 |
| DIS | 3.665 | 4 | MO | 4.105 | 5 |
| EK | 3.876 | 4 | MRK | 4.421 | 8 |
| GE | 4.591 | 5 | MSFT | 3.583 | 4 |
| GM | 5.342 | 6 | PG | 3.743 | 4 |
| HD | 3.494 | 4 | SBC | 4.440 | 5 |
| HON | 4.455 | 5 | T | 2.947 | 3 |
| HPQ | 3.437 | 4 | UTX | 3.532 | 5 |
| IBM | 3.992 | 6 | WMT | 3.501 | 5 |
| INTC | 3.807 | 5 | XOM | 4.389 | 5 |
Согласно таблице 4, почти половина исследуемых рядов имеют значение корреляционной размерности меньше 4, и, следовательно, можно предположить, что их динамика представлена маломерными хаотическими детерминированными системами. Это, в свою очередь, дает основание применять к исследуемым временным рядам другие инструменты теории нелинейной динамики и хаоса.
FNN-анализ
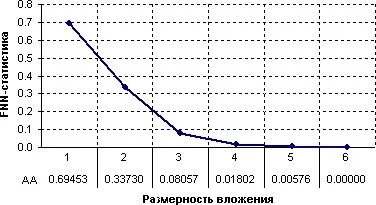
Выполнение FNN-анализа может быть проведено с помощью программных продуктов CDA, Dataplore и Tisean. Основным недостатком пакета Tisean является отсутствие графического интерфейса, что, тем не менее, не умаляет правильности заложенных в них алгоритмов, подробно описанных в [13]. Подробно останавливаться на описании результатов обработки стилизованных данных всеми программными продуктами не будем, отметим, тем не менее, что, как и в предыдущих разделах, CDA и Dataplore на выходе часто дают труднообъяснимые результаты, поэтому от использования этих программ было решено отказаться. Подробное описание метода приведено выше, в теоретической части работы. Применим FNN-анализ к стилизованным данным систем Хенона и Лоренца, кроме того, исследуем зависимость результата анализа при добавлении шума к ряду, порожденному отображением Хенона (рис. 3-5). Здесь по оси абсцисс отложены значения размерности вложения, а по оси ординат — значения отношения числа ложных соседей ко всем. Теоретически, для ряда, порожденного отображением Хенона значение этого отношения (FNN-статистики) должно обнуляться при достижении размерности вложения m=2, для ряда, порожденного системой Лоренца — при m=4. Кроме того, при добавлении шума должно наблюдаться увеличение значения размерности вложения, при которой FNN-статистика становится равной нулю. Убедимся, что результаты, полученные с помощью программы Tisean, вполне соответствуют теоретическим (рис. 3-4).
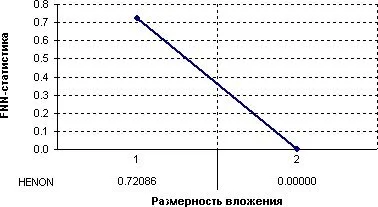
Несмотря на тот факт, что результат для стилизованных данных практически идеален, необходимо, тем не менее, с осторожностью подходить к анализу реальных данных. Как уже было отмечено, в настоящее время не существует явного критерия, который смог бы объяснить, какое значение отношения числа ложных соседей ко всем соседям является «достаточно малым», чтобы можно было принять гипотезу о достаточном значении размерности вложения. Напомним, в теоретической части работы было сделано предположение, что гипотезу о достаточности величины размерности вложения можно принимать при определенном уровне ее значимости. Ее эмпирическое построение будет предложено после анализа полученных значений. Также напомним гипотезу о том, что значение размерности вложения, при которой число ложных соседей становится равным нулю, а, следовательно, и отношение числа ложных соседей ко всем становится равным нулю, определяет верхнюю границу значения искомой размерности псевдоаттрактора, что также далее будет обсуждаться после анализа полученных результатов.
На рисунке 4 приведен один из графиков зависимости FNN-статистики от размерности вложения для исследуемых в работе временных рядов. По оси абсцисс отложены значения размерности вложения, по оси ординат — значения отношения числа ложных соседей к их общему количеству.
Полученные с помощью FNN-анализа оценки значения размерности вложения mFNN занесем в таблицу (табл. 5). Напомним, что согласно сделанному ранее предположению, значение размерности вложения, при которой число ложных соседей становится равным нулю, а, следовательно, и отношение числа ложных соседей ко всем становится равным нулю, определяет верхнюю границу значения искомой размерности псевдоаттрактора.
Также в таблице приведем значения оценки размерности вложения mкорр, полученные в результате оценки корреляционной размерности. Как и ожидалось, для некоторых котировок (например, MO, T, PG) наблюдаются очень долгие осцилляции около нулевого значения. Для того чтобы сформулировать критерий, по которому оценку размерности можно считать релевантной при ненулевом значении FNN-статистики, поступим следующим образом. Сначала выделим временные ряды, для которых оценки размерности вложения mFNN и mкорр отличаются больше, чем на единицу (эти временные ряды выделены в таблице серым цветом).
Затем для выделенных рядов будем по рисунку будем подбирать такое значение размерности вложения mFNN, чтобы оно было максимально близким к значению mкорр, полученному в результате оценки корреляционной размерности. Если при этом окажется, что значения FNN-статистик большинства исследуемых временных рядов, соответствующие выбранным mFNN, будут меньше некоторого достаточного малого числа, то это число, предположительно, может быть выбрано в качестве уровня значимости FNN-статистики. Это даст нам удобный критерий для определения достаточной размерности вложения.
| Компания | mкорр | mFNN | mFNN | Значение FNN-статистики |
| AA | 4 | 6 | 5 | 0.005 |
| AXP | 7 | 8 | 8 | 0.000 |
| BA | 5 | 15 | 6 | 0.002 |
| С | 8 | 8 | 8 | 0.000 |
| CAT | 8 | 9 | 8 | 0.003 |
| DD | 7 | 7 | 7 | 0.000 |
| DIS | 4 | 8 | 5 | 0.003 |
| EK | 4 | 11 | 6 | 0.004 |
| GE | 5 | 8 | 5 | 0.002 |
| GM | 6 | 11 | 6 | 0.003 |
| HD | 4 | 10 | 5 | 0.005 |
| HON | 5 | 7 | 5 | 0.002 |
| HPQ | 4 | 9 | 5 | 0.006 |
| IBM | 6 | 8 | 6 | 0.002 |
| INTC | 5 | 7 | 5 | 0.002 |
| IP | 6 | 6 | 6 | 0.000 |
| JNJ | 6 | 7 | 7 | 0.000 |
| JPM | 4 | 7 | 5 | 0.004 |
| KO | 3 | 10 | 5 | 0.004 |
| MCD | 7 | 8 | 8 | 0.000 |
| MMM | 10 | 9 | 9 | 0.000 |
| MO | 5 | 19 | 6 | 0.002 |
| MRK | 8 | 6 | 6 | 0.000 |
| MSFT | 4 | 6 | 5 | 0.001 |
| PG | 4 | 12 | 5 | 0.004 |
| SBC | 5 | 6 | 6 | 0.000 |
| T | 3 | 20 | 6 | 0.004 |
| 0UTX | 5 | 9 | 5 | 0.005 |
| WMT | 5 | 7 | 6 | 0.003 |
| XOM | 5 | 7 | 5 | 0.003 |
Согласно результатам, приведенным в таблице, значения FNN-статистик всех исследуемых временных рядов, кроме HPQ, получились меньше 0.005. Это означает, что если предложенная гипотеза о существовании уровня значимости FNN — статистики правильна, то для исследуемых данных уровень значимости FNN-статистики p=0.005. Отсюда получаем простой механизм определения размерности вложения из FNN-анализа для реальных данных. После получения графика зависимости FNN-статистики от размерности вложения для исследуемого временного ряда, проведем горизонтальную прямую, которая соответствует значению уровню значимости (в нашем случае, p=0.005). Эта прямая пересечет график значений FNN-статистики в некоторой точке m0. Если m0совпало с целым значением размерности вложения, то построенное таким образом значение размерности вложения совпадает с ее истинным значением m=m0. В противном случае размерность вложения следует считать равной ближайшему целому значению размерности m, большей, чем m0.
Полученные в результате исследования ложных соседей подтвердили результаты оценки размерности вложения с помощью корреляционной размерности, что еще раз подтверждает наличие маломерной хаотической составляющей в анализируемых временных рядах и является сильным обоснованием применения методов нелинейной динамики и теории хаоса к исследованию финансовых инструментов.