Моделирование процесса релаксации давления в полости плоской геометрии после ее опрессовки

Оперативный контроль коллекторских характеристик прискважинной зоны позволяет оптимизировать процессы эксплуатации газовых месторождений и, тем самым, увеличивать продолжительность и эффективность эксплуатации скважин [2, 4-7]. Работа посвящена исследованию релаксации давления в полости, заполненной газом и окруженной насыщенной газом пористой средой, после ее опрессовки.

Основные уравнения. Пусть в исходном состоянии (t0, а сама полость заполнена газом (рис. 1). В момент времени t=0 в полость дополнительно вводится газ и давление в ней мгновенно достигает значения p₀. Далее за счет фильтрации газа в окружающее пористое пространство давление в полости стремится к значению p'₀.

При описании этих процессов скелет пористой среды будем считать несжимаемым и однородным, а коэффициент вязкости газа не зависящим от температуры и давления. В рамках вышеизложенных допущений, учитывая, что изменение массы газа в полости происходит только за счет фильтрации газа через стенки полости в окружающую пористую среду, запишем уравнение сохранения массы газа в следующем виде:

$\frac {d\rho_g}{dt}= \frac {1}{a}\rho _{g} \upsilon$,

где a — толщина трещины; $\rho_g$ — плотность газа; $\upsilon$ — скорость фильтрации газа через стенки полости.

Давление в окружающей полость пористой среде будем описывать с помощью нелинейного уравнения пьезопроводности [1]:

$\frac{\partial p'}{\partial t}= \frac{k}{m\mu_g} \frac{\partial}{\partial x}\bigg(p'\frac{\partial p'}{\partial x}\bigg), a$.

Здесь $\mu_g$ — коэффициент динамической вязкости газа; p' — давление газа вокруг полости; m и k — коэффициенты пористости и проницаемости окружающей полость пористой среды.

Учитывая, что в исходном состоянии давление газа во всем пористом пласте вокруг полости постоянно и равно начальное условие для уравнения (2) запишем в виде:

$p'=p'_{0}, (t=0, x>a)$.

На стенке полости выполняется условие равенства давлений справа и слева

$p'=p(t), (t>0, x=a)$.

где p(t) — давление внутри полости.

Второе граничное условие для уравнения (2) имеет вид:

$p'=p'_{0}, (t>0, x\rightarrow \infty)$.

Аналитическое решение нелинейного уравнения пьезопроводности общего вида для фильтрации газа (2) при условиях (3) — (5) не найдено. В работе это уравнение будем использовать в линеаризованном приближении. Для этого перепишем уравнение (2) в виде:

$\frac{1}{p'} \frac{\partial (p')^j}{\partial t}= \frac{k}{m\mu_g} \frac{\partial^2(p')^j}{\partial x^2}$,

где значения показателя степени j = 1 и 2 соответствуют обычной линеаризации и линеаризации по Лейбензону [3]. Заметим, что изменение p' мало относительно среднего значения этой величины, поэтому коэффициент при $\frac{\partial (p')^j}{\partial t}$ в левой части уравнения (6) можно считать постоянным.

Таким образом, если во всей области течения и для всех значений t величина p' мало отклоняется от своего начального значения, то уравнение (6) можно переписать в виде

$\frac{\partial (p')^j}{\partial t}= \kappa_g\frac{\partial^2(p')^j}{\partial x^2}, \kappa_g=\frac{kp'_{0}}{m\mu_g}$,

где $\kappa_g$ — коэффициент пьезопроводности.

Для фильтрации газа в пористой среде вокруг полости используем закон Дарси:

$\upsilon'=-\frac{k}{\mu_g }\frac{\partial p'}{\partial x}, a$,

где $\upsilon'$ — скорость фильтрации газа вокруг полости. Граничное условие для уравнения (8) имеет вид:

$\upsilon'=\upsilon, (t>0, x=a)$.

Для замыкания системы уравнений (1), (7) и (8), считая, что газ является калорически совершенным, запишем связь текущих значений плотности и давления в полости:

$\frac {p}{p_0} = \bigg(\frac {\rho_{g} } {\rho_{g0} }\bigg)^\gamma$,

где $\gamma$ — показатель политропы, $\rho_{g0}$ — начальное значение плотности газа в полости.

Подставляя в уравнение (1) величину $\rho_g$ из (9), получим:

$\frac {1} {p} \frac {dp}{dt}= -\frac{\gamma}{a} \upsilon$.

Уравнение (10) связывает давление внутри полости со скоростью фильтрации газа через ее стенки.

После некоторых преобразований в работе получены нелинейные интегральные уравнения, описывающие эволюцию давления внутри полости:

$\ln \frac{p}{p_0}=- \frac {k\gamma}{a\mu_g\sqrt{ \pi\kappa_g}} \int^{t}_{0}\frac {p(t')-p'_{0}}{\sqrt{t — t'}} dt', j=1$,

$p =p_0 — \frac {k\gamma}{2a\mu_g\sqrt{ \pi\kappa_g}} \int^{t}_{0}\frac {(p(t'))^2-(p'_{0})^{2}}{\sqrt{t-t'}} dt', j=2$.

Для дальнейшего анализа эти уравнения удобно представить в безразмерной форме:

$\ln \frac{P}{P_0}=- \frac {m\gamma}{\sqrt{ \pi}} \int^{t}_{0}\frac {P(\tau') — 1}{\sqrt{\tau — \tau'}} d\tau', j=1$,

$P=P_0 — \frac {m\gamma}{2\sqrt{ \pi}} \int^{t}_{0}\frac {(P(\tau'))^2-1}{\sqrt{\tau -\tau'}} d\tau', j=2$,

где $P= \frac {p}{p'_0}$, $t = \tau t_{ag}$, $t'= \tau' t_{ag}$, $t_{ag}=\frac {a^2}{\kappa _g}=\frac{a^2\mu_g m}{k p'_{0}}$, $P_0=\frac {p_0}{p'_0}$, $\tau= \frac {\pi}{\gamma^{2}m^2}\tilde{ \tau}$.

Результаты численного расчета приведены на рис. 2. Здесь представлены зависимости безразмерного давления P от безразмерного времени $\tilde{ \tau}$, полученные в результате численного решения интегральных уравнений (12). Линии 1 и 2 соответствуют значениям P₀ =5 и 2. Cплошные линии получены при обычной линеаризации, а пунктирные линии — при линеаризации по Лейбензону.

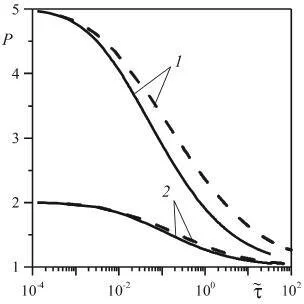
Из рис. 2 видно, что при описании процесса фильтрации с помощью уравнения пьезопроводности, линеаризованного по Лейбензону, восстановление давления происходит медленнее. С уменьшением разности между начальным значением давления в полости и значением давления вокруг полости отличия между решениями, полученными двумя способами линеаризации уравнения пьезопроводности, тоже уменьшаются (линии 2).

В результате исследований установлено:

• время релаксации давления в полости имеет обратную зависимость от коэффициента проницаемости;
• разница между решениями, полученными двумя способами линеаризации уравнения пьезопроводности, уменьшается с уменьшением начальной депрессии.