Отражение акустических волн от пористой преграды с «открытой» границей

Пористые материалы во многих случаях применяются в звукопоглощающих облицовках производственных помещений и технических устройств, требующих снижения уровня шумов.

Звукопоглощающая способность пористых материалов обусловлена их пористой структурой и наличием большого числа открытых сообщающихся между собой пор, максимальный диаметр которых обычно не превышает 2 мм. Большая удельная поверхность материалов, создаваемая стенками открытых пор, способствует активному преобразованию энергии звуковых колебаний в тепловую энергию вследствие потерь на трение. Упругие свойства скелета материала и наличие воздуха, заключённого в его порах, обусловливают гашение энергии удара и вибрации, что способствует снижению структурного и ударного шума [1, 6, 7].

В данной работе рассматривается отражение акустических волн от пористой преграды с «открытой» границей (рис. 1). Когда граница «открытая», то газ, содержащийся в порах, расположенных непосредственно на границе, соприкасается с флюидом, окружающим пористую преграду.

Пусть акустическая волна, распространяясь по флюиду, воздействует на плоскую поверхность пористой преграды, насыщенной газом. Толщина пористой преграды равна l, а высота и ширина достаточно большие, чтобы не учитывать краевые эффекты. Поверхность преграды, на которую воздействует волна, будем считать первой границей, а параллельную ей поверхность, расположенную на расстоянии l, — второй границей.

Найдем коэффициенты отражения и прохождения волны. Пусть гармоническая плоская волна с круговой частотой $\omega$, распространяясь по однородному флюиду, падает перпендикулярно первой границе «флюид — пористая среда». Тогда движение слева от границы (xυ\upsilon которых определяются по формулам

$p_{e}^{(o)} =A_{p,e}^{(o)} \exp \left[i\cdot \left(K_{e} x-\omega \cdot t\right)\right]$, $\upsilon _{e}^{(o)} =A_{\upsilon, e}^{(o)} \exp \left[i\cdot \left(K_{e} x-\omega \cdot t\right)\right]$ [1]

$p_{e}^{(r)} =A_{p,e}^{(r)} \exp \left[i\cdot \left(-K_{e} x-\omega \cdot t\right)\right]$, $\upsilon _{e}^{(r)} =A_{\upsilon, e}^{(r)} \exp \left[i\cdot \left(-K_{e} x-\omega \cdot t\right)\right]$ [2]

Волновые числа «быстрой» K_a и «медленной» K_b волн вычислялись для трех случаев с учетом:

1. Межфазных сил;
2. Межфазного теплообмена;
3. Межфазных сил и межфазного теплообмена [6, 7].

Нижний индекс e соответствует параметрам волны, распространяющейся по флюиду, а верхние индексы o, r — параметрам падающей и отраженной волн. Амплитуды давления A_p,e^(m) и скорости $A_{\upsilon, e}^{(m)}$ (m=o, r) падающей и отраженной гармонических волн связаны соотношениями

$A_{p,e}^{(o)} =\rho _{e0}^{0} C_{e} A_{\upsilon, e}^{(o)}, A_{p,e}^{(r)} =-\rho _{e0}^{0} C_{e} A_{\upsilon, e}^{(r)}$ [3]

Здесь $\rho _{e0}^{0}$ — плотность флюида, окружающего пористую среду, C_e — скорость распространения волны во флюиде, K_e — волновое число.

При падении волны из флюида на пористую среду в однородной среде возникает отраженная волна [2 — 5], а в пористой среде — прошедшая волна, представляющая собой суперпозицию двух волн — «быстрой» и «медленной». Для определения коэффициентов отражения и прохождения падающей волны запишем граничные условия, количество которых должно соответствовать количеству возникающих волн. На границе x=0$ должны выполняться следующие условия:

1. непрерывность давления на границе между окружающим преграду флюидом и газом, находящимся в открытых порах на границе:

p_e =p_g [4]

2. непрерывность нормальной компоненты усредненной по объему скорости на поверхности раздела:

$\upsilon _{e} =\alpha _{g0} \upsilon _{g}^{} +\alpha _{s0} \upsilon _{s}^{}$ [5]

3. равенство сил, действующих на единицу площади поверхности (т.е. суммарные напряжения), по обе стороны от этой поверхности:

$p_e =-\sigma _s^\ast +p_g$ [6]

Здесь $p_{e} =p_{e}^{\left(0\right)} +p_{e}^{\left(r\right)}$, $\upsilon _{e} =\upsilon _{e}^{\left(0\right)} +\upsilon _{e}^{\left(r\right)}$ — результирующие возмущение давления и скорость частиц на границе со стороны однородной среды соответственно.

Результирующие возмущения эффективного напряжения в скелете $\sigma _s^\ast$ и давления в газовой фазе определяются по формулам

$\sigma _s^\ast=\left[A_{\sigma, a} \exp \left(iK_{a} x\right)+A_{\sigma, b} \exp \left(iK_{b} x\right)\right]\exp \left(-i\omega \, t\right)$ [7]

$p_{g} =\left[A_{p,a} \exp \left(iK_{a} x\right)+A_{p,b} \exp \left(iK_{b} x\right)\right]\exp \left(-i\omega \, t\right)$ [8]

Здесь $A_{\sigma a}A_{p,a}$ и $A_{\sigma b}A_{p,b}$ — соответственно амплитуды напряжения и давления «быстрой» и «медленной» волн, распространяющихся по скелету и газовой фазе. Нижние индексы a и b соответствуют параметрам «быстрой» и «медленной» волн.

Результирующие скорости движения скелета и газа в порах находятся из выражений

$\upsilon _{s} =\left[A_{s,a} \exp \left(iK_{a} x\right)+A_{s,b} \exp \left(iK_{b} x\right)\right]\exp \left(-i\omega t\right)$ [9]

$\upsilon _{g} =\left[A_{g,a} \exp \left(iK_{a} x\right)+A_{g,b} \exp \left(iK_{b} x\right)\right]\exp \left(-i\omega t\right)$ [10]

Зависимости амплитуд возникающих волн от амплитуды падающей волны определены из граничных условий и уравнений движения. После этого найдем коэффициенты отражения N₁^(op) и прохождения «медленной» M_b и «быстрой» M_a волн на первой границе «флюид — пористая преграда»:

$M_{b} =2\left[1-z_{b}/z_{a}+\psi (C_{b}-C_{a}z_{b}/z_{a})\right]$ [11]

$M_{a}=2/\left[1-z_{a}/z_{b}+\psi (C_{a}-C_{b}z_{a}/z_{b})\right]$ [12]

$N_{1}^{\left(op\right)} =M_{b} +M_{a} -1$ [13]

Здесь параметры $\psi$, C_j, z_j, B₁, $\beta$ и $\xi$ определяются из выражений

$\psi =\alpha_{g0}(1+\chi_{T})\rho _{e0}^{0} C_{e}/\rho _{g0}^{0}C_{g}^{2}, C_{j} =\omega /K_{j}$,

$z_j =-\chi _{\mu} C_{s}^{2} \left(B_1/C_g^2-1/C_j^2\right)/\beta\xi\left(1+i\chi_V\right), j=a,b$,

$B_{1} =\left(1+\chi _{T} \right)\left(1+i\chi _{V} \alpha _{s0} \right), \beta =\rho _{g0}^{0} /\rho _{s0}^{0}, \xi =\alpha _{s0}^{0} /\alpha _{g0}^{0}$.

Здесь $\alpha _{g0}$ — начальная объемная доля газовой фазы, $\alpha _{s0}$ — начальная объемная доля твердой фазы. Коэффициент $\chi _{\mu }$ учитывает влияние вязкости материала скелета пористой среды на эволюцию «быстрой» и «медленной» волн. Коэффициент $\chi _{T}$ учитывает влияние теплообмена между скелетом и газом, насыщающим поры среды, на динамику «быстрой» и «медленной» волн, распространяющихся в пористой среде. Влияние нестационарных сил межфазного взаимодействия на динамику «быстрой» и «медленной» волн учитывается величиной $\chi _{V}$.

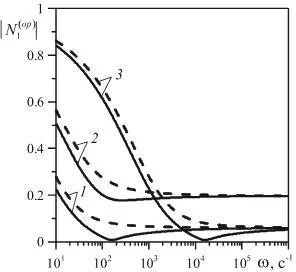
На рис. 2 представлены результаты расчетов, полученные по формулам [11] — [13]. Параметры фаз взяты при температуре среды 300K и давлении p₀ =10⁵ Па. Преграда находится в воздухе. Штриховые линии на рис. 2 соответствуют случаю, когда в расчетах учитываются лишь межфазные силы, т.е. получены без учета межфазного теплообмена, а сплошные линии построены с учетом межфазных сил и межфазного теплообмена. Линии 1, 2 и 3 соответствуют следующим случаям: линии 1 — радиус пор a₀ =10^-3м, содержание объемной доли газа $\alpha _{g0} =0.9$, линии 2 — a₀ =10^-3м, $\alpha _{g0} =0.7$, линии 3 — a₀ =10^-4 м, $\alpha _{g0} =0.9$.

Расчеты показали, что во всем частотном диапазоне действительная часть коэффициента отражения величина положительная. В области низких частот $\omega$ с уменьшением радиуса пор среды модуль коэффициента отражения увеличивается. В области высоких частот модуль коэффициента отражения слабо зависит от радиуса пор среды. Уменьшение содержания объемной доли газа приводит к увеличению модуля коэффициента отражения во всем частотном диапазоне. Межфазный теплообмен лишь незначительно уменьшает модуль коэффициента отражения.

Таким образом, для гашения шумовых эффектов от низкочастотных волн лучше всего использовать мелкодисперсные пористые материалы.